锐角三角形的内接三角形的周长最小值分析
写于
2022.3.29
初中几何的三大动点极值问题,即将军饮马、胡不归、阿氏圆,早已被研究透彻,福建中考也不愿考阿氏圆这样的区分度太高的题.
锐角三角形的内接三角形的周长最小值,也可以套作将军饮马的变种,并不难分析. 本文将浅显地给出思路和结论.
题目
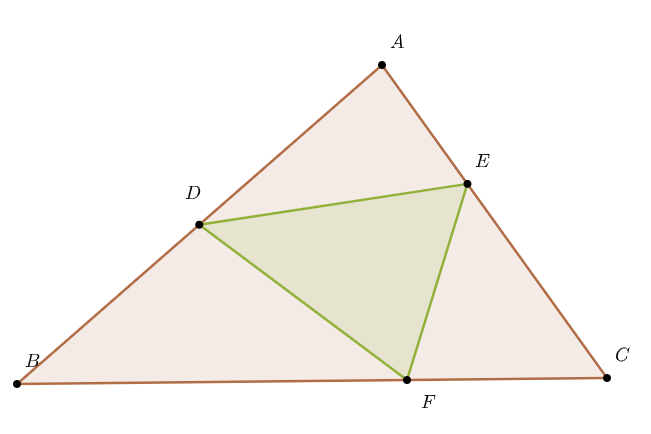
如果一个三角形的三个顶点分别在另一个三角形的三条边上,则该三角形称为另一个三角形的内接三角形.
如图,$△ABC$是一个锐角三角形,$△DEF$是它的一个内接三角形,试分析$C_{△DEF}$的最小值在何时取到.
分析
首先将点E视为一定点,并去掉一些线段. 如图所示,这时$C_{△DEF}$的最小值是否很眼熟?
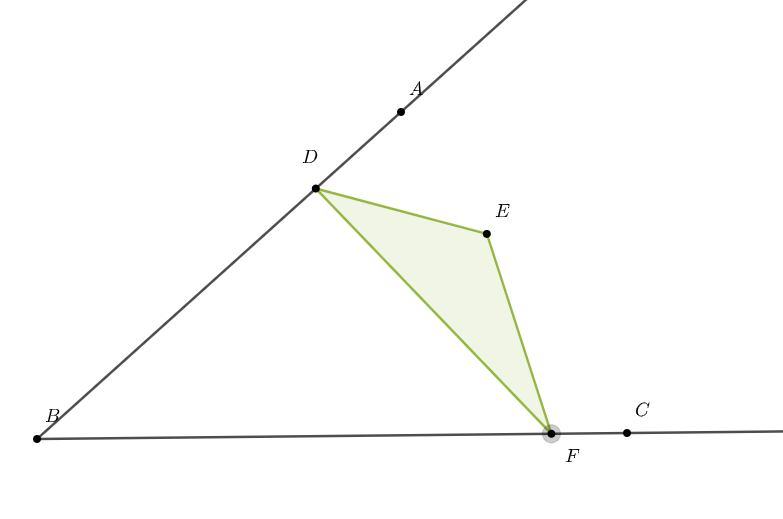
这显然就是角内部的将军饮马模型,我们知道要分别作出 点$E$关于直线$BA$、$BC$的对称点$E_1$、$E_2$.
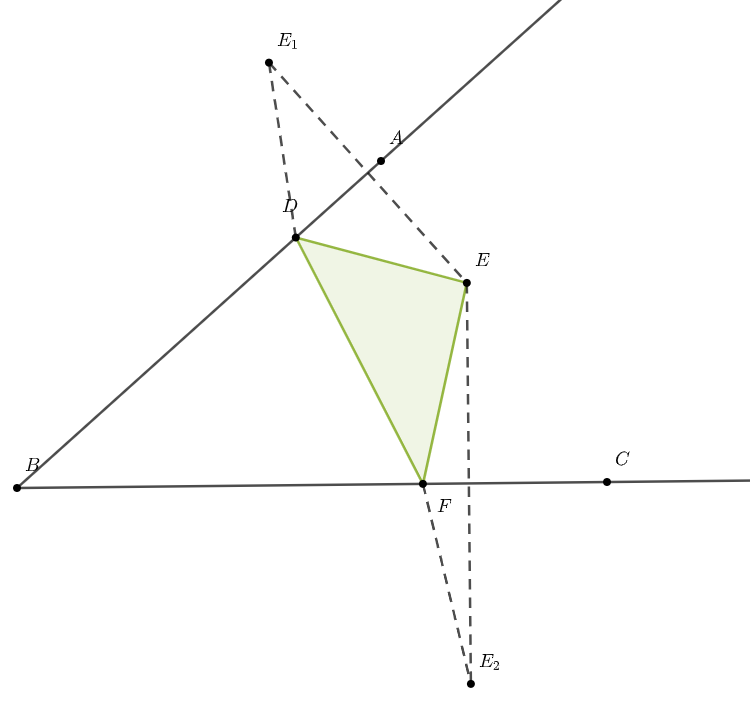
那么$C_{△DEF}=ED+EF+DF=E_1D+E_2F+DF\leq E_1E_2$ (当且仅当点$D$、$F$在直线$E_1E_2$上时取等).
现在把三角形搬回来,考虑点$E$为动点时,$E_1E_2$的最小值.
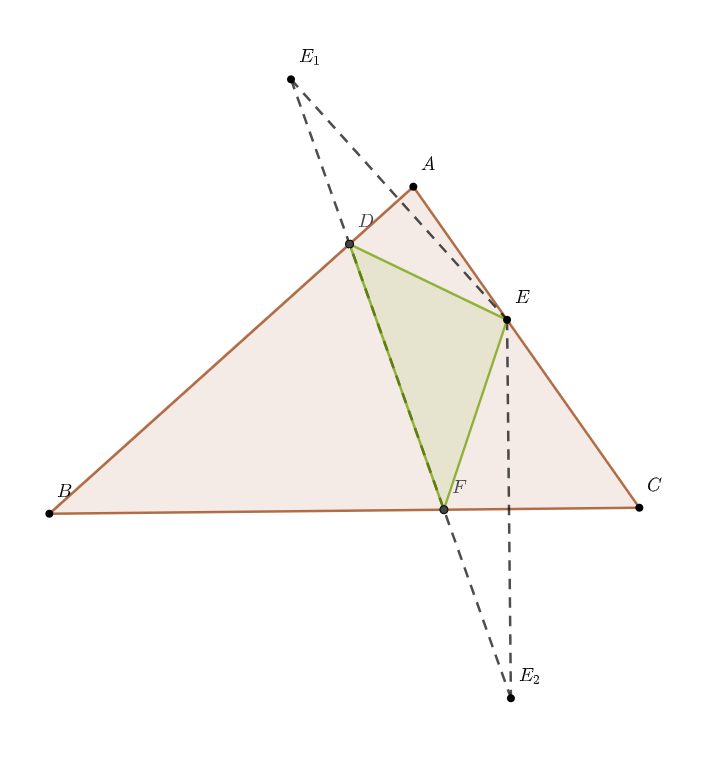
先说结论,$E_1E_2\propto BE$!($\propto即“正比于”$)
怎么推导的呢?连接$BE_1、BE_2$,过点$B$作$BT\perp E_1E_2$于点$T$.
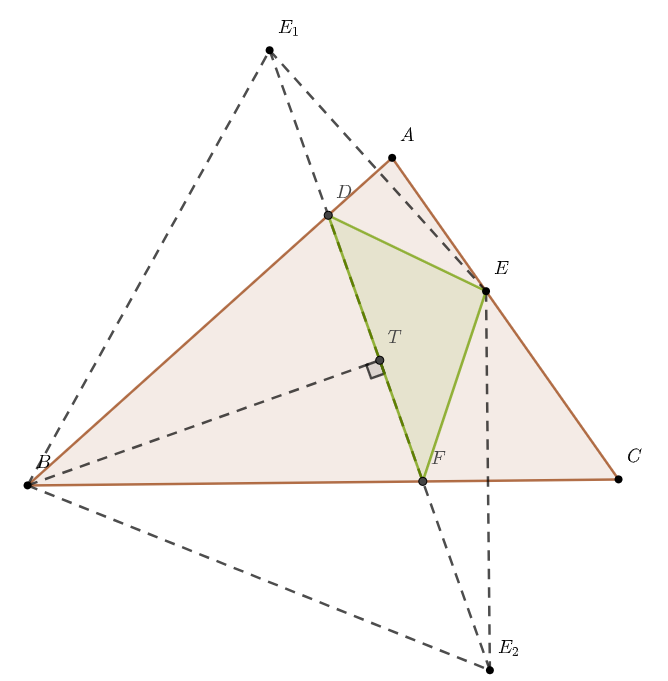
由对称可以推出$BE_1=BE_2=BE$,$\angle ABC = \frac{1}{2} \angle E_1BE_2$.
所以在等腰$△E_1BE_2$中,$\angle E_1BT=\frac{1}{2} \angle E_1BE_2 = \angle ABC$.
所以$E_1E_2=2E_1T=2 \cdot BE_1\sin\angle E_1BT=2\sin\angle ABC \cdot BE$.
由于$\angle ABC$为定角,所以$\sin\angle ABC$为定值,那么$E_1E_2\propto BE$(比例系数为$2\sin\angle ABC$).
所以$BE\perp AC$时,$BE$最小,$E_1E_2$也就最小,于是$C_{△DEF}$取得了最小值.
由于你可以把$D$、$E$、$F$中的任意一点视为定点来走以上分析过程,所以可以推知此时$BE$、$AF$、$AD$都为$△ABC$的高,即$△DEF$为$△ABC$的 “垂足三角形”!
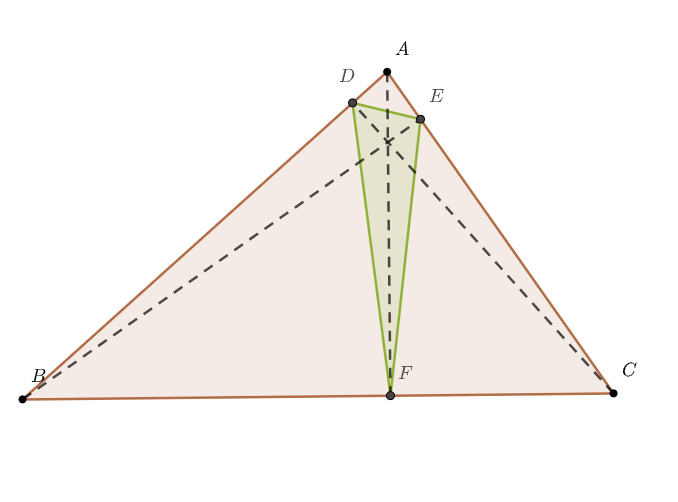
这就是我们的结论(施瓦兹三角形问题的结论):
\[在锐角三角形的所有内接三角形中,以垂足三角形的周长为最短.\]本文分析到这里还有很多遗漏的点,可惜没时间再作探讨,有兴趣可以自己讨论垂足三角形的更多几何性质.
♥