两直线垂直，斜率相乘为什么等于 -1？如果夹角是其他角度呢？
写于
2021.12.12
解析几何告诉我们，平面直角坐标系中的两条直线，如果相互垂直，那么它们的斜率相乘等于-1.
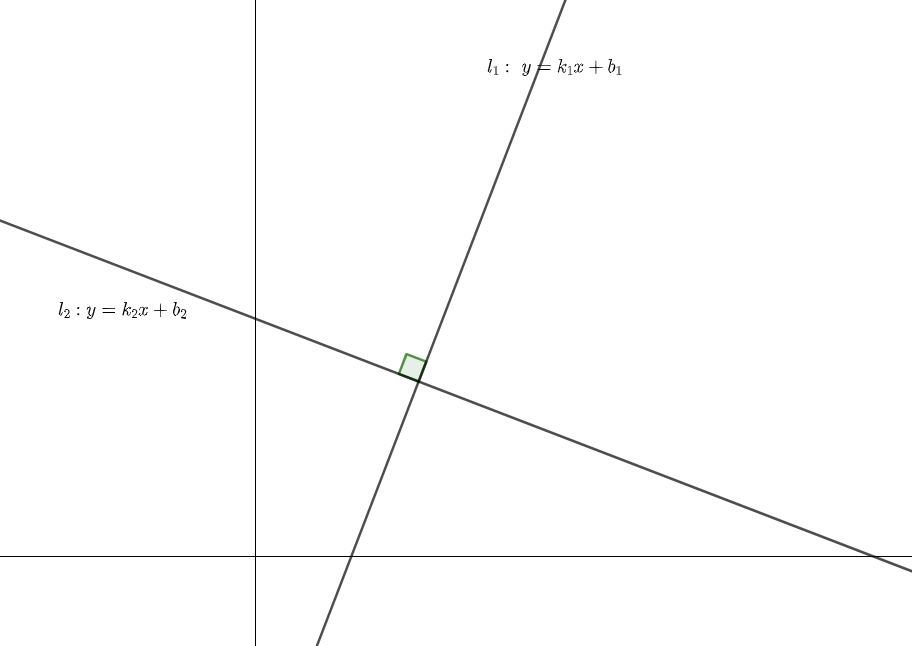如图，$l_1\perp l_2$，则必有$k_1k_2=-1$.
下面给出初中方法的证明.
Part 1 前置条件
首先需要证明， 若斜率存在，则 $l_a\parallel l_b \Rightarrow k_a=k_b$. 此结论未出现在初中课本上.
令 $l_a:y=k_ax+p ,\ \ l_b:y=k_bx+q$.
假设$k_a \ne k_b$.
联立两条直线，得 $k_ax+p=k_bx+q$.
解得 $x=\frac{q-p}{k_a-k_b}$.
由于$k_a\ne k_b$，所以 $x$ 的分母不为 $0$ ，也就是说，实数 $x$ 一定存在. 而且这里的 $x$ 同时满足两条直线方程.
由于两条直线平行，所以它们不存在交点，也就不存在能同时满足两条直线方程的实数$x$.
这就产生了矛盾.于是必有 $k_a=k_b$.
Part 2 几何证明
事实上，中考中需要使用$k_1k_2=-1$的地方，经常可以构造一线三垂直的相似来代替.
经过了Part 1的证明，我们可以光明正大地把两条垂直的直线平移到原点处了，因为平移过后斜率根本不会发生改变，我们可以把任意直线垂直的证明等价为原点处的两条直线.
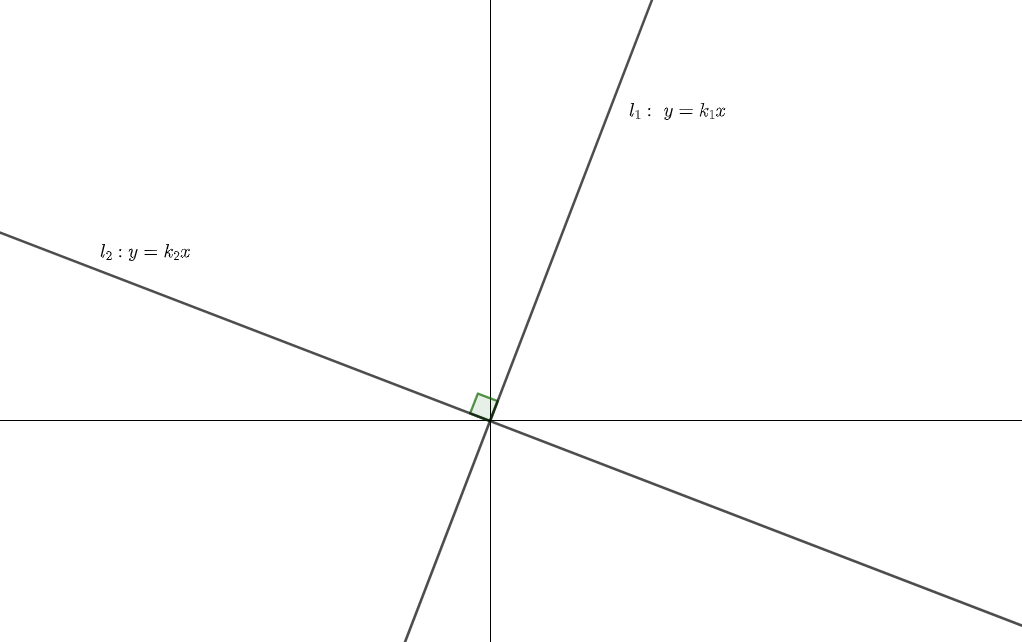
不妨直接构造一线三垂直的全等.
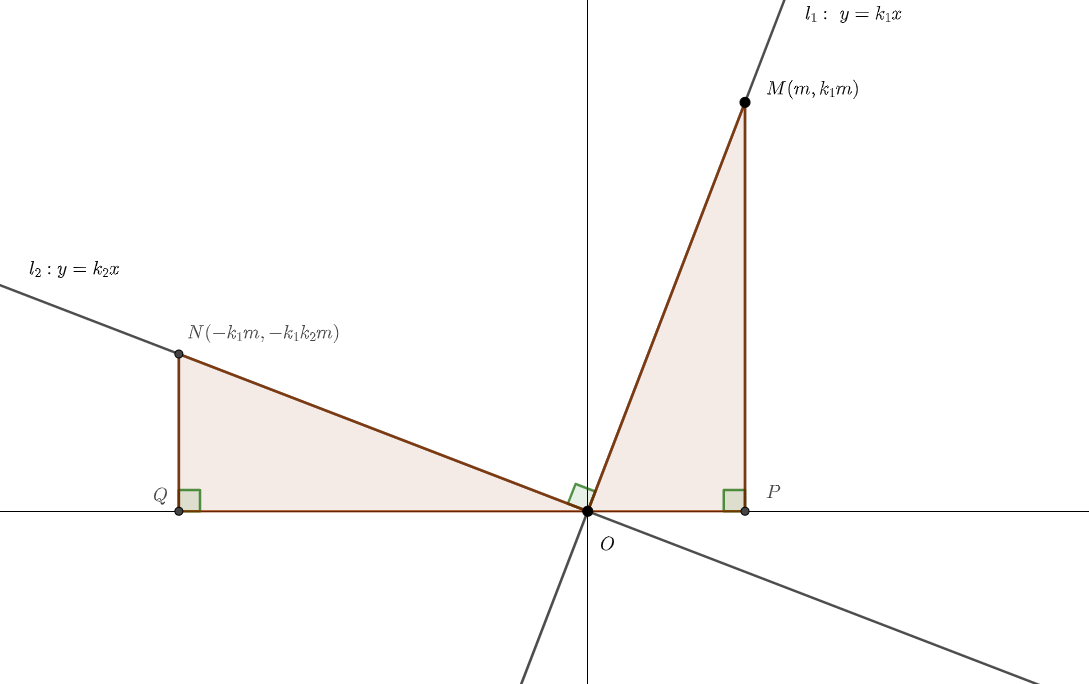在$l_1$上取一点$M(m,k_1m)$.
为了构造全等，在$x$轴上取一点$Q$，使$OQ=MP$，并过点$Q$作$x$轴垂线交$l_2$于点$N$. 则$x_N=-y_M=-k_1m$.
再代入$l_2$解析式，所以$N(-k_1m,-k_1k_2m)$. 所以$NQ=y_N=-k_1k_2m$.
容易看出，$△NQO\cong△OPM(ASA)$.
所以$NQ=OP$.
代入，得$-k_1k_2m=m$.
即证$k_1k_2=-1$.
Part 3 三角函数证明
直线的斜率正是倾斜角的正切值，那么为什么不用和差角公式证明呢？
以下的同乘、同除是基于倾斜角不会是0度或90度，即它们的正弦、余弦和正切都不会是0.
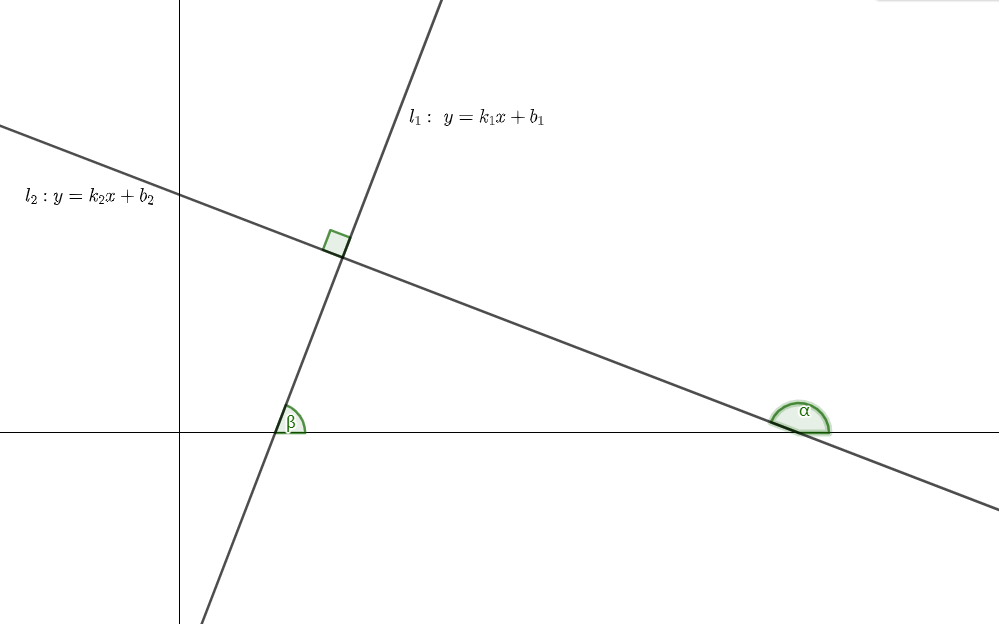由三角形外角公式，显然$\alpha-\beta=90°$.
那么$cos(\alpha-\beta)=cos \ 90°=0$.
展开，得 $cos\alpha cos\beta +sin\alpha sin\beta = 0$.
两边同除 $sin\alpha cos\beta$，得 $\frac{1}{tan\alpha}+tan\beta=0$.
两边同乘 $tan\alpha$，得 $1+tan\alpha tan\beta=0$.
又因为$tan\alpha =k_2, tan\beta = k_1$,
即证$k_1k_2=-1$.
Part 4 夹角公式
若两直线夹角为$\theta$，那么有$tan\theta = \frac{k_1-k_2}{1+k_1k_2}$. 事实上，这就是正切的差角公式.
那么在夹角为$90°$时，$\tan 90°$无意义，则$1+k_1k_2=0$. 亦印证了$k_1k_2=-1$..
Part 5 向量验证(2022.7.8补充)
取直线 $l_1:y=k_1x$， $l_2:y=k_2x$ 的方向向量分别为$\boldsymbol{a} = (1,k_1)$, $\boldsymbol{b} = (1,k2)$.
由于$l_1\perp l_2$，有$\boldsymbol{a}\perp \boldsymbol{b}$，所以$\boldsymbol{a} \cdot \boldsymbol{b}=0$，即$1\times1+k_1k_2=0$，亦即$k_1k_2=-1$.
本篇就到此结束.
♥