射影定理的三种证明
射影定理是初中数学中一个重要的定理,却不包含在人教版数学课本中。
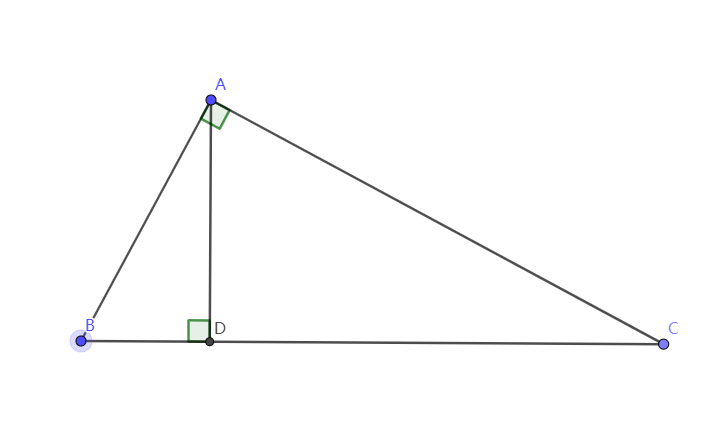
如图,在 Rt△ ABC 中,AD 是斜边 BC 上的高 。则有射影定理如下:
\(\begin{align} AB^2=BD\times BC \\ AC^2=CD\times CB \\ AD^2=BD\times CD \end{align}\) 这里列举三种证明方法。
\[\begin{align} &\text{(一)锐角三角函数证明(强烈推荐,实际书写很快):}\\ &\text{显然}\cos B=\frac{BD}{AB}=\frac{AB}{BC} \\ &\text{即 } AB^2=BD\times BC&(1)\\ &\text{同理,有 }AC^2=CD\times CB&(2)\\ &\text{显然 }\angle CAD=\angle B\\ &\text{所以 } \tan\angle CAD=\tan\angle B\\ &\text{所以 } \frac{AD}{CD}=\frac{BD}{AD}\\ &\text{所以 } AD^2=BD\times CD&(3)\\ &\text{(二)相似证明(常规):}\\ &\text{易证} \triangle BAC \sim \triangle BDA \sim \triangle ADC \text{ , 则有}\\ &\frac{BA}{BD}=\frac{BC}{BA}, \frac{AC}{DC}=\frac{BC}{AC},\frac{BD}{AD}=\frac{DA}{DC}\\ &\text{即}AB^2=BD\times BC,AC^2=CD\times CB,AD^2=BD\times CD\\ &\text{(三)勾股定理证明:}\\ (1) &\text{根据勾股定理, }BD^2+AD^2=AB^2,\\ &AD^2+CD^2=AC^2\\ &\text{两式相加, }2AD^2+BD^2+CD^2=AB^2+AC^2\\ &\text{由于}AB^2+AC^2=BC^2\\ &\text{所以}2AD^2=BC^2-BD^2-CD^2 \\&=(BD+CD)^2-BD^2-CD^2 \\&=BD^2+CD^2+2BD\times CD-BD^2-CD^2 \\&=2BD\times CD\\ &\text{所以}AD^2=BD\times CD. \\ (2)&\text{已证明}AD^2=BD\times CD\\ &\text{所以}AD^2+BD^2=BD\times CD+BD^2\\ &\text{所以}AB^2=BD\times(CD+BD)=BD\times BC.\\ (3)&\text{同(2).} \end{align}\]这篇文章对我是LaTeX的练习。
♥