OI笔记 | 2023.4-6 做题记录(一)
好吧,4-6 月都特别摆。省选后洛谷做题量单调递减,只有共 $27+16+8=51$ 题。
暑期前的学习计划也没完成。该学的算法没学,该补的题也没补。
期末考成绩出来并不理想,然后一度想要 AFO。和教练讨论后,又想到自己之前的某些信念,还是决定继续学一学。
其实学 OI 挺开心的,对吧。
嗑瓜子
现在有一堆共 $n$ 粒瓜子。每次吃一个瓜子会产生两个瓜子壳。
每次从堆中拿取一个物品。如果拿到瓜子就吃掉,并把产生的两个瓜子壳丢进堆中。如果拿到瓜子壳就直接扔掉。
每次拿到每一粒瓜子或者是瓜子壳的概率是均等的,问期望多少次能够把瓜子拿完。
$n \le 2\times 10^3$
题解
这明显是一个期望 dp。
考虑一种暴力的状态设计,即设 $dp_{i,j}$ 为目前有 $i$ 个瓜子和 $j$ 个壳的状态下的期望步数。
相当于在 DAG 上转移,一个点的期望为后继点的期望加边权再乘上走这条边的概率:
\[E(u)=\sum\limits_{edge(u,v)} P(edge)\times (E(v)+w(edge))\]所以本题的 $dp$ 式子为:
\[dp_{i,j}=\frac{i}{i+j} \times (dp_{i-1,j+2} + 1) + \frac{j}{i+j}\times (dp_{i,j-1} + 1)\]参考代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
const int MOD = 998244353, MAX_N = 2e3 + 10;
int n;
ll inv[MAX_N << 2], dp[MAX_N][MAX_N << 1];
int main() {
n = read();
inv[1] = 1;
for(int i = 2; i <= 4 * n; i++)
inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;
for(int i = 1; i <= n; i++) {
dp[i][0] = (dp[i - 1][2] + 1) % MOD;
for(int j = 1; j <= 2 * n; j++) {
(dp[i][j] += (dp[i - 1][j + 2] + 1) * i % MOD * inv[i + j] % MOD) %= MOD;
(dp[i][j] += (dp[i][j - 1] + 1) * j % MOD * inv[i + j] % MOD) %= MOD;
}
}
write(dp[n][0]);
return 0;
}
Tallest Cow
有 $N$ 头牛站成一行,被编队为 $1,2,\cdots N$,每头牛的身高都为整数。
当且仅当两头牛中间的牛身高都比它们矮时,两头牛方可看到对方。
现在,我们只知道其中最高的牛是第 $P$ 头,它的身高是 $H$,剩余牛的身高未知。
但是,我们还知道这群牛之中存在着 $M$ 对关系,每对关系都指明了某两头牛 $A$ 和 $B$ 可以相互看见。
求每头牛的身高的最大可能值是多少。
题解
题意即 $A,B(A\le B)$ 能相互看见的充要条件为 $\forall i \in [A+1,B-1], H_i\le \min(H_A,H_B)$。
那么我们可以假设所有牛的初始高度都为 $H$,然后把所有区间 $[A+1,B-1]$ 减一即可贪心地满足题意。
可以用差分来实现。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
const int MAX_N = 5005, MAX_M = 10005;
int n, p, H, m;
int h[MAX_N];
pii s[MAX_M];
int main() {
n = read(), p = read(), H = read(), m = read();
for(int i = 1, l, r; i <= m; i++) {
l = read(), r = read();
if(l > r) swap(l, r);
s[i].first = l, s[i].second = r;
}
sort(s + 1, s + m + 1);
m = unique(s + 1, s + m + 1) - s - 1;
for(int i = 1, l, r; i <= m; i++) {
l = s[i].first, r = s[i].second;
h[l + 1]--, h[r]++;
}
for(int i = 1; i <= n; i++) {
h[i] += h[i - 1];
write(h[i] + H);
putchar('\n');
}
return 0;
}
[NOIP2012 提高组] 国王游戏
恰逢 H 国国庆,国王邀请 $n$ 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 $n$ 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数 $a$ 的乘积除以他自己右手上的数 $b$,然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
$1 ≤ n ≤1,000,0 < a,b < 10000$。
题解
考虑贪心,只需将大臣按 $a\times b$ 从小到大排序即可。
考虑使用微扰法证明。
我们现在交换两个相邻的大臣 $i, i + 1$。
交换前,$i$ 获得的奖励为 $\frac{1}{b_i}\times \prod\limits_{j=0}^{i-1} a_j$,$i + 1$ 获得的奖励为$\frac{1}{b_{i+1}}\times \prod\limits_{j=0}^{i} a_j$
交换后,$i$ 获得的奖励为 $\frac{1}{b_{i+1}}\times \prod\limits_{j=0}^{i-1} a_j$,$i + 1$ 获得的奖励为$\frac{a_{i+1}}{b_i}\times \prod\limits_{j=0}^{i-1} a_j$
由于其他大臣获得的奖励不会改变,我们只需比较交换前后这两个人获得奖励的最大值。提取公因式后,只需比较下列式子:
\[\max(\frac{1}{b_i},\frac{a_i}{b_{i+1}}), \max(\frac{1}{b_{i+1}},\frac{a_{i+1}}{b_i})\]变为乘积式:
\[\max(b_{i+1}, a_i \times b_i ), \max(b_i, a_{i + 1}\times b_{i + 1})\]由于 $a_{i}\times b_i \ge b_i, a_{i + 1}\times b_{i + 1}\ge b_{i + 1}$,上式 相当于比较:
\[a_{i}\times b_i, a_{i + 1}\times b_{i + 1}\]所以如果 $a_{i}\times b_i\le a_{i + 1}\times b_{i + 1}$,交换前更优。如果 $a_{i}\times b_i> a_{i + 1}\times b_{i + 1}$,交换后更优。因此,总是让 $a\times b$ 小的在前面更优。
然后这题注意写一个效率正常的高精度即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pii;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
struct BigNum {...};
BigNum max(BigNum A, BigNum B) {...}
const int MAX_N = 1005;
ll n, l, r;
pii a[MAX_N];
inline bool cmp(pii x, pii y) { return x.first * x.second < y.first * y.second; }
int main() {
n = read();
l = read(), r = read();
for(ll i = 1; i <= n; i++)
a[i].first = read(), a[i].second = read();
sort(a + 1, a + n + 1, cmp);
BigNum Ans = BigNum(1);
BigNum Mul = BigNum(l);
for(ll i = 1; i <= n; i++) {
Ans = max(Ans, Mul / a[i].second);
Mul = Mul * BigNum(a[i].first);
}
Ans.out();
return 0;
}
费解的开关
$25$ 盏灯排成一个 $5×5$ 的方形。每一个灯有开关两种状态。
每一步,游戏者可以改变某一个灯的状态,同时和这个灯上下左右相邻的灯也要相应地改变其状态。
给定游戏的初始状态,编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。
$0<n≤500$
题解
Flip Game 是一个很经典的问题。在这个游戏中,显然灯的状态与按钮按下的先后无关,只与哪些按钮被按下了有关。可见,一个按钮不可能按下两次,因为这相当于没有按按钮,还浪费了步数。
它有以下几种常见的算法:
-
朴素暴力枚举 $\mathcal{O}(n^2 \times 2^{n^2})$:枚举每一个格子是否点击,然后检验操作后棋盘是否合法。
-
首行暴力枚举 $\mathcal{O}(n\times 2^n)$:枚举首行的每一个格子是否点击,然后依次转移到下一行。由于当前行的点击状态确定后,为了让当前行的每个灯都亮着,下一行的相同列的位置是否点击也确定了。最后只需要检验最后一行的灯是否都亮着。
-
完全方程法 $\mathcal{O}(n^6)$ :一个灯的状态则是由它和它周围 $4$ 个按钮决定的,设灯 $(i,j)$ 的初始状态为 $a_{i,j}$,最终状态为 $b_{i,j}$,每个按钮的状态为 $x_{i,j}$。则有:
所以,用高斯消元解 $n^2$ 元一次异或方程组即可。
- 首行方程法 $\mathcal{O}(n^3)$,这里不介绍,可以看知乎上的那篇专栏。
对于本题,使用方法 $2$ 即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
inline bool read_bool() {...}
const int MAX_N = 7;
int T, ans;
bool a[MAX_N][MAX_N], t[MAX_N][MAX_N];
void change(int x, int y) {
t[x][y] ^= 1;
t[x - 1][y] ^= 1;
t[x + 1][y] ^= 1;
t[x][y - 1] ^= 1;
t[x][y + 1] ^= 1;
}
int cal(int state) {
int cnt = 0;
for(int i = 1; i <= 5; i++)
for(int j = 1; j <= 5; j++)
t[i][j] = a[i][j];
for(int i = 1; i <= 5; i++)
if((state >> (i - 1)) & 1) change(1, i), cnt++;
for(int i = 2; i <= 5; i++)
for(int j = 1; j <= 5; j++)
if(!t[i - 1][j]) change(i, j), cnt++;
for(int i = 1; i <= 5; i++)
if(!t[5][i]) return -1;
return cnt;
}
int main() {
T = read();
while(T--) {
ans = -1;
for(int i = 1; i <= 5; i++)
for(int j = 1; j <= 5; j++)
a[i][j] = read_bool();
for(int i = 0, now; i < (1 << 5); i++) {
now = cal(i);
if(now != -1) ans = (ans == -1 ? now : min(ans, now));
}
if(ans > 6) ans = -1;
write(ans);
putchar('\n');
}
return 0;
}
[省选联考 2023] 火车站
$1\sim n$ 的数轴上有 $m$ 个区间 $[l_i,r_i]$。
现在有一动点 $P$ 从位置 $x$ 出发,朝着某一方向移动,且移动方向始终不变。
设 $P$ 的位置为 $t$,则每时每刻点 $P$ 必须选择一个包含 $t$ 的区间作为它的移动范围。若 $P$ 到达它选择的移动范围的端点,则它停止移动。同时,若某时刻 $t$ 被其他区间包含,则它可以选择换一个包含 $t$ 的区间作为移动范围。
求出所有 $P$ 停止移动的位置。
$1 \le n, m \le 2 \times 10^5$,$1 \le x \le n$,$1 \le l_i < r_i \le n$。
题解
在草稿纸上模拟题意:
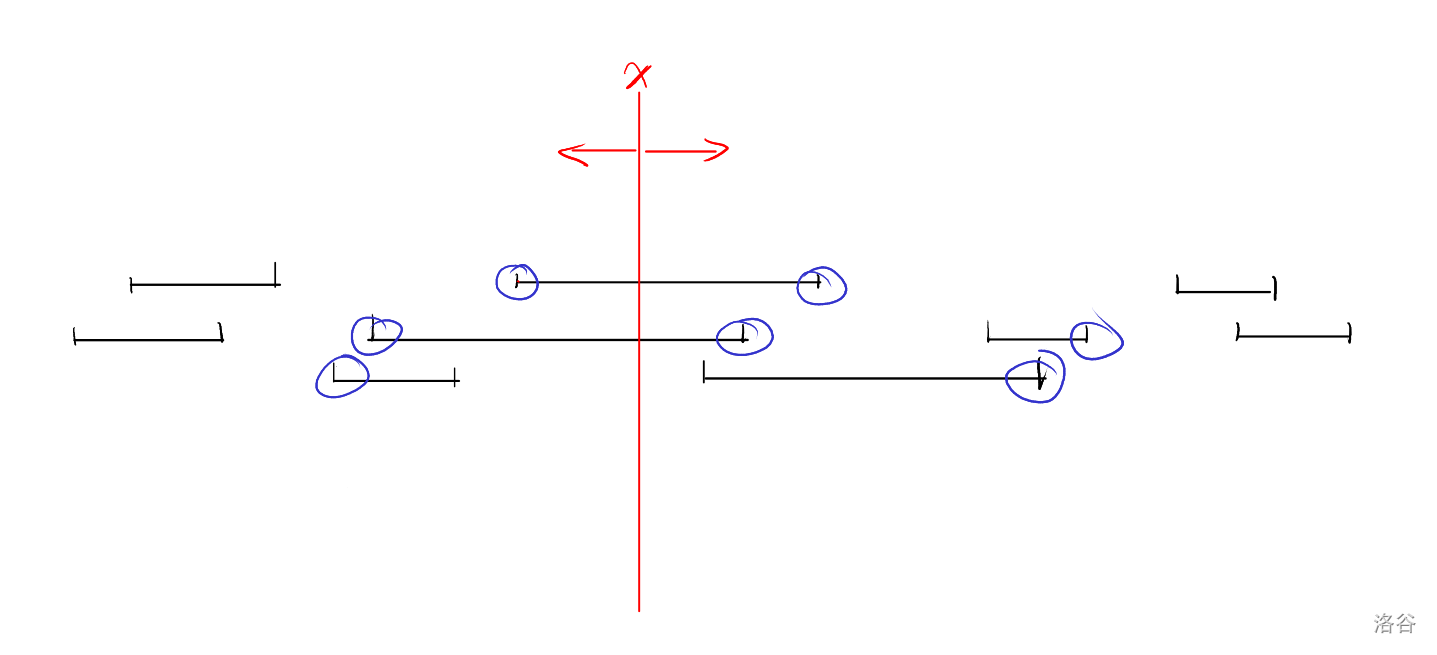
容易发现,题意其实就是找到 $x$ 所在的连通块。连通块包含的铁路的左端点只要在 $x$ 左边即可纳入答案,右端点只要在 $x$ 右边即可纳入答案。
连通块可以用并查集维护。
具体的,我们把区间排序后额外加入一个区间 $[x,x]$ 并编号,便于之后用并查集找到 $x$ 点所在的集合。然后从左到右做区间并,把相交的区间并入同一个集合。
然后再扫一遍区间得到答案。
时间复杂度 $\mathcal{O}(m\log m)$。
参考代码:
#include <bits/stdc++.h>
#define pb emplace_back
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
const int MAX_N = 5e5 + 10;
int n, m, x, cnt, L, R;
pii line[MAX_N];
int fa[MAX_N], ans[MAX_N];
inline bool check(pii x, pii y) {
int l1 = x.first, r1 = x.second;
int l2 = y.first, r2 = y.second;
return (r1 >= l2 && l1 <= r2);
}
inline int find(int x) {
if(fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
inline void merge(int x, int y) {
fa[find(x)] = find(y);
}
int main() {
n = read(), m = read(), x = read();
for(int i = 1; i <= m; i++)
line[i].first = read(), line[i].second = read();
line[++m] = make_pair(x, x);
sort(line + 1, line + m + 1);
m = unique(line + 1, line + m + 1) - line - 1;
for(int i = 1; i <= m; i++)
fa[i] = i;
L = line[1].first, R = line[1].second;
for(int i = 2, lst = 1; i <= m; i++) {
if(check(make_pair(L, R), line[i])) {
merge(i, lst);
R = max(R, line[i].second);
}
else {
L = line[i].first;
R = line[i].second;
lst = i;
}
}
int pos = lower_bound(line + 1, line + m + 1, make_pair(x, x)) - line;
int fx = find(pos);
for(int i = 1, l, r; i <= m; i++)
if(i != pos && find(i) == fx) {
l = line[i].first, r = line[i].second;
if(l < x) ans[++cnt] = l;
if(r > x) ans[++cnt] = r;
}
sort(ans + 1, ans + cnt + 1);
cnt = unique(ans + 1, ans + cnt + 1) - ans - 1;
for(int i = 1; i <= cnt; i++)
write(ans[i]), putchar(' ');
putchar('\n');
return 0;
}
安全系统
有两种球,分别是黑球和白球,同色的球都是相同的。现在有 $a$ 个黑球和 $b$ 个白球,要放进 $n$ 个不同的盒子。每个盒子可以装任意多的球,也可以不装;每个球也可以不放进任何盒子里。求方案总数。
题解
我们考虑只有黑球的情况,设 $f(i)$ 为 $i$ 个黑球全部放入盒子里的方案数 $(0\le i \le a)$,则黑球的方案数为:
\[\sum_{i=0}^a f(i)\]考虑插板法,这里每个盒子都可以为空,所以我们添加 $n$ 个虚拟的球,则有 $n+i-1$ 个空位,隔 $n-1$ 个板。所以有
\[f(i) = \binom{n+i-1}{n-1}\]考虑用递推公式
\[\binom{n}{i}=\binom{n-1}{i} +\binom{n-1}{i-1}\]化简答案:
\[\sum_{i=0}^a\binom{n+i-1}{n-1}=\sum_{i=0}^a \binom{n+i}{n} - \sum_{i=0}^a \binom{n+i-1}{n}\\ = \sum_{i=1}^{a+1} \binom{n+i-1}{n} - \sum_{i=0}^a\binom{n+i-1}{n}\\=\binom{n+a}{a}\]所以可以 $\mathcal{O}(a+b)$ 计算答案:
\[\binom{n+a}{a}\times \binom{n+b}{b}\]代码如下:
#include <bits/stdc++.h>
using namespace std;
typedef __int128 ll;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
int n, a, b;
ll C(int n, int m) {
ll ret = 1;
for(int i = 1; i <= m; i++) {
ret *= n - i + 1;
ret /= i;
}
return ret;
}
int main() {
n = read(), a = read(), b = read();
write(C(n + a, a) * C(n + b, b));
return 0;
}
子集和
你有 $n$ 个正整数 $a_1,a_2,\dots,a_n$,它们的和是 $m$。你想对它们的每个子集 $S$, 求出它们的和。
现在你得到了 $2^n$ 个 $[0,m]$ 之间的和, 其中数字 $i$ 出现了 $b_i$ 次。
现在给你数组 $b_i$, 请还原 $a_1,a_2,\dots,a_n$ 这些数。
题解
我们从小到大枚举 $i$,每当我们遇到 $b_i>0$,不断把 $i$ 加入答案。
加入答案的同时,我们把 $i$ 产生的贡献减掉。这一步只需要从小到大枚举 $j\in [i,m]$,执行 $b_j\gets b_j - b_{j-i}$。
这样一来,枚举到 $i$ 时,比 $i$ 小的数对 $i$ 产生的贡献已经消失,如果 $b_i$ 仍然大于 $0$,则只能是 $i$ 自己构成的子集。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
int n, m, tot, ans[55], b[10005];
int main() {
n = read(), m = read();
for(int i = 0; i <= m; i++)
b[i] = read();
for(int i = 1; i <= m; i++) {
while(b[i] > 0) {
for(int k = i; k <= m; k++)
b[k] -= b[k - i];
ans[++tot] = i;
}
}
for(int i = 1; i <= tot; i++)
write(ans[i]), putchar(" \n"[i == tot]);
return 0;
}
另一种理解是,考虑这道题的逆序,子集求和。这个可以直接用 01 背包来做,转移方程为 $dp_i=\sum dp_{i-j}$。所以考虑把代码逆序即可。
♥