OI笔记 | 2023.3 做题记录
[Ynoi Easy Round 2021] TEST_152
转转有一个操作序列$(l_i,r_i,v_i)$。
现在,有 $q$ 个询问 $l$,$r$。
每次询问,你初始有一个长度为 $m$ 的序列 $c$,初值全是 $0$。
现在我们从 $l$ 到 $r$ 执行这 $r-l+1$ 个操作。
每个操作是将 $c[l_i]$~$c[r_i]$ 赋值为 $v_i$。
询问所有操作结束后整个 $c$ 的序列所有数的和。
询问之间互相独立。
$ 1 \le n,m,q \le 5 \times 10^5$
题解
考虑将询问离线,按 $r$ 排序,套扫描线,即把 $\le r$ 的操作执行后,询问 $\ge l$ 的操作所影响的和。这个维度可以用树状数组。
然后区间颜色段可以用 set 维护,时间复杂度 $O(n\log n)$。
#include <bits/stdc++.h>
#define pb emplace_back
using namespace std;
typedef long long ll;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
const int MAX_N = 5e5 + 10;
int n, m, q;
ll ans[MAX_N];
struct node {
int l, r, v, i;
node(int _l = 0, int _r = 0, int _v = 0, int _i = 0) :
l(_l), r(_r), v(_v), i(_i) {}
bool operator < (const node &t) const {return r < t.r;}
} a[MAX_N], t[MAX_N];
set<node> s;
typedef set<node>::iterator iter;
struct TreeArray {
ll t[MAX_N];
TreeArray() {memset(t, 0, sizeof(t));}
inline int lowbit(int i) {return i & -i;}
inline void add(int i, ll v) {
if(!i) return;
for(; i <= n; i += lowbit(i))
t[i] += v;
}
inline ll query(int i) {
ll ret = 0;
for(; i; i -= lowbit(i))
ret += t[i];
return ret;
}
} tree;
void split(iter a, int pos) {
int l = a -> l, r = a -> r, v = a -> v, i = a -> i;
if(pos <= l - 1 || pos >= r) return;
s.erase(a);
s.insert(node(l, pos, v, i));
s.insert(node(pos + 1, r, v, i));
}
void assign(int l, int r, int v, int i) {
iter x = s.lower_bound(node(0, l - 1, 0, 0));
split(x, l - 1);
iter y = s.lower_bound(node(0, r, 0, 0));
split(y, r);
x = s.lower_bound(node(0, l, 0, 0));
y = s.lower_bound(node(0, r + 1, 0, 0));
for(iter i = x; i != y; ) {
iter j = i;
tree.add(j -> i, - 1ll * ((j -> r) - (j -> l) + 1) * (j -> v));
i++;
s.erase(j);
}
s.insert(node(l, r, v, i));
tree.add(i, 1ll * (r - l + 1) * v);
}
int main() {
n = read(), m = read(), q = read();
for(int i = 1; i <= n; i++)
a[i].l = read(), a[i].r = read(), a[i].v = read();
for(int i = 1; i <= q; i++)
t[i].l = read(), t[i].r = read(), t[i].i = i;
sort(t + 1, t + q + 1);
s.insert(node(1, m, 0, 0));
for(int i = 1, now = 1; i <= q; i++) {
while(now <= t[i].r) {
assign(a[now].l, a[now].r, a[now].v, now);
now++;
}
ans[t[i].i] = tree.query(n) - tree.query(t[i].l - 1);
}
for(int i = 1; i <= q; i++)
write(ans[i]), putchar('\n');
return 0;
}
[APIO2010] 巡逻
在一个地区中有 $n$ 个村庄,编号为 $1, 2, \dots, n$。有 $n-1$ 条道路连接着这些村庄,每条道路刚好连接两个村庄,从任何一个村庄,都可以通过这些道路到达其他任何一个村庄。每条道路的长度均为 $1$ 个单位。为保证该地区的安全,巡警车每天要到所有的道路上巡逻。警察局设在编号为 $1$ 的村庄里,每天巡警车总是从警察局出发,最终又回到警察局。下图表示一个有 $8$ 个村庄的地区,其中村庄用圆表示(其中村庄 $1$ 用黑色的圆表示),道路是连接这些圆的线段。为了遍历所有的道路,巡警车需要走的距离为 $14$ 个单位,每条道路都需要经过两次。
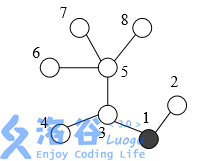
为了减少总的巡逻距离,该地区准备在这些村庄之间建立 $K$ 条新的道路,每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束,如下面的图例 (c)。一条新道路甚至可以是一个环,即其两端连接到同一个村庄。由于资金有限,$K$ 只能是 $1$ 或 $2$。同时,为了不浪费资金,每天巡警车必须经过新建的道路正好一次。下图给出了一些建立新道路的例子:
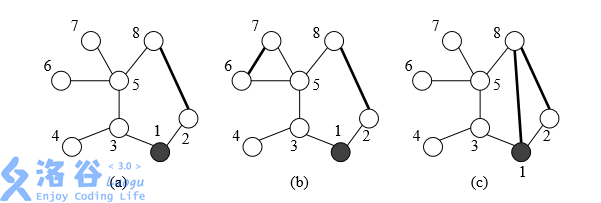
在 (a) 中,新建了一条道路,总的距离是 $11$。在 (b) 中,新建了两条道路,总的巡逻距离是 $10$。在 (c) 中,新建了两条道路,但由于巡警车要经过每条新道路正好一次,总的距离变为了 $15$。试编写一个程序,读取村庄间道路的信息和需要新建的道路数,计算出最佳的新建道路的方案使得总的巡逻距离最小,并输出这个最小的巡逻距离。
$3≤n≤10^5,1≤K≤2$。
题解
当 $k = 0$ 时,最小的巡逻距离为 $2(n-1)$,这是因为每条边都要经过至少两次。
首先考虑 $k = 1$ 的情况。当我们加了一条边 $(u, v)$ 后,因为题中指出“要经过每条新道路正好一次”,所以我们从 $u$ 到 $v$ 后,必须要从原图中 $v$ 到 $u$ 的路径走回来。那么有 $dis(u,v)$ 条边少走了一遍,多走了这条新的边。答案的变化量即为 $-dis(u, v) + 1$。
要最小化答案, 那么 $dis(u, v)$ 要尽量大,最大即为树的直径 $L_1$。所以 $k=1$ 的答案为 $2(n-1)-L_1+1 = 2n-L_1-1$。
再考虑 $k = 2$ 的情况。我们在与原来直径尽量不重叠的地方再找一条最长链,在最长链的两端添加边。算法的具体实现,可以把原来的直径上的边的边权设为 $-1$,再用树形 dp 来求直径即可。设新的直径为 $L_2$,则答案为 $2n +(-L_1+1)+(-L_2+1)=2n-L_1-L_2$。
注意后一次求直径不能用 dfs。我们设边权为 $-1$ 是为了重叠部分计算成经过两遍,而 dfs 会受负边权影响。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {
ll ret = 0, w = 1; char c = getchar();
while(!isdigit(c)) {if(c == '-') w = -1; c = getchar();}
while(isdigit(c)) {ret = (ret << 1) + (ret << 3) + (c ^ 48); c = getchar();}
return ret * w;
}
char buf[50];
inline void write(ll x) {
if(x < 0) putchar('-'), x = -x;
int tp = 0;
do { buf[++tp] = x % 10 + 48; x /= 10;} while(x);
while(tp) putchar(buf[tp--]);
}
const int MAX_N = 2e5 + 10;
int n, k;
int tot = 1, ver[MAX_N], nxt[MAX_N], fir[MAX_N], e[MAX_N];
int mx, l1, l2, L1, L2, dep[MAX_N], f[MAX_N];
void AddEdge(int u, int v, int w) {
ver[++tot] = v;
e[tot] = w;
nxt[tot] = fir[u];
fir[u] = tot;
}
void dfs(int u, int fa, int &dmax, int &l) {
if(dep[u] > dmax) {
dmax = dep[u];
l = u;
}
for(int i = fir[u]; i; i = nxt[i]) {
int v = ver[i], w = e[i];
if(v == fa) continue;
dep[v] = dep[u] + w;
dfs(v, u, dmax, l);
}
}
bool sign(int u, int fa) {
if(u == l2) return true;
bool ret = false;
for(int i = fir[u]; i; i = nxt[i]) {
int v = ver[i];
if(v == fa) continue;
if(sign(v, u)) ret = true, e[i] = e[i ^ 1] = -1;
}
return ret;
}
int cal() {
memset(dep, 0, sizeof(dep)); mx = 0; dfs(1, 0, mx, l1);
memset(dep, 0, sizeof(dep)); mx = 0; dfs(l1, 0, mx, l2);
return mx;
}
void dp(int u, int fa, int &ans) {
for(int i = fir[u]; i; i = nxt[i]) {
int v = ver[i], w = e[i];
if(v == fa) continue;
dp(v, u, ans);
ans = max(ans, f[v] + f[u] + w);
f[u] = max(f[u], f[v] + w);
}
f[u] = max(f[u], 0);
ans = max(ans, f[u]);
}
int main() {
n = read(), k = read();
for(int i = 1, u, v; i <= n - 1; i++) {
u = read(), v = read();
AddEdge(u, v, 1);
AddEdge(v, u, 1);
}
L1 = cal();
if(k == 1) write(2 * n - 1 - L1), putchar('\n');
else {
sign(l1, 0);
dp(1, 0, L2);
write(2 * n - L1 - L2), putchar('\n');
}
return 0;
}
循环依赖
在 Excel 中,我们可以在一个表格中键入公式,当键入公式时,我们首先先打出一个等号,接下来输入公式来表示如何计算该单元格的内容。
我们通常使用列号(大写字母串)和行号(数字)连接来引用一个单元格的内容,比如 B23、AA2,在一个单元格中,可以键入诸如 =A1+A2 的公式,表示对 A1 单元格和 A2 单元格内的数字求和,这样该单元格的值就依赖于 A1 与 A2 两个单元格的值,如果我们在 B1 单元格中键入该公式,那么我们就有 B1=A1+A2,随着 A1和 A2 单元内数值的变化,B1单元格内数值也会随之变化,同时 B1 也能作为其它单元格所引用的对象,比如 C1 单元格内可以键入 =B1*A1。
但现在,如果我们在 A2 单元格中键入=C1-A1,那么为了求解 A2,需要先求解其一个依赖 C1,为了求解 C1 需要求解其一个依赖 B1,而求解 B1 又要求解其一个依赖 A2,这样就产生了一个循环依赖关系,而 Excel 没有解方程的功能,因此这种情况下单元格的值无法得出,更一般地,如果在求解任意一个单元格的过程中,沿某条依赖关系能走到该单元格本身,那么就产生一个循环依赖关系。
现在给定一张 Excel 表格中每个单元格引用其它单元格的引用列表,你的任务就是判断其中是否存在循环依赖关系。
题解
拓扑排序板子。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
const int MAX_N = 1e5 + 10;
int T, n, tot, cnt, in[MAX_N];
string s, y[20];
unordered_map<string, int> mp;
vector<int> G[MAX_N];
void split(string s) {
int r = 0, len = s.length();
while(r < len) {
string tmp;
while(r < len && s[r] != ' ') tmp += s[r], r++;
y[++cnt] = tmp;
r++;
}
}
int id(string s) {
if(mp[s]) return mp[s];
return mp[s] = ++tot;
}
bool topo() {
int tmp = 0;
queue<int> q;
for(int i = 1; i <= tot; i++)
if(!in[i]) q.push(i);
while(!q.empty()) {
int u = q.front(); q.pop();
tmp++;
for(int v : G[u])
if(--in[v] == 0) q.push(v);
}
return tmp == tot;
}
int main() {
freopen("dependency.in", "r", stdin);
freopen("dependency.out", "w", stdout);
T = read();
while(T--) {
n = read(), tot = 0;
mp.clear();
memset(in, 0, sizeof(in));
for(int i = 1; i <= n; i++) {
getline(cin, s);
cnt = 0;
split(s);
int u = id(y[1]);
for(int j = 2; j <= cnt; j++) {
int v = id(y[j]);
G[u].push_back(v); in[v]++;
}
}
puts(topo() ? "No" : "Yes");
for(int i = 1; i <= tot; i++)
G[i].clear();
}
fclose(stdin);
fclose(stdout);
return 0;
}
[JLOI2011] 飞行路线
Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 $n$ 个城市设有业务,设这些城市分别标记为 $0$ 到 $n-1$,一共有 $m$ 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 $k$ 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
$2 \le n \le 10^4$,$1 \le m \le 5\times 10^4$,$0 \le k \le 10$,$0\le s,t,a,b\le n$,$a\ne b$,$0\le c\le 10^3$。
题解
考虑建一个分层图,共有 $k + 1$ 层。
每层之间的连边的边权都是 $0$。
那么向下一层相当于用一次免费的机会。
答案即为 $\min\limits_{i\in [0, k]}(dis_{s, t+i\cdot n})$。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
inline ll read() {...}
inline void write(ll x) {...}
const int MAX_N = 1e4 + 10, MAX_M = 5e4 + 10;
int n, m, k, s, t, cnt, ans, dis[MAX_N * 15];
bool vis[MAX_N * 15];
struct edge {
int v, w, nxt;
edge(int _v = 0, int _w = 0, int _nxt = 0) :
v(_v), w(_w), nxt(_nxt) {}
} E[MAX_M * 50];
int fir[MAX_N * 15];
inline void AddEdge(int u, int v, int w) {
E[++cnt] = edge(v, w, fir[u]);
fir[u] = cnt;
}
void dijkstra(int s) {
priority_queue<pii, vector<pii>, greater<pii>> q;
memset(dis, 127, sizeof(dis));
dis[s] = 0;
q.push(make_pair(0, s));
while(!q.empty()) {
int u = q.top().second; q.pop();
if(vis[u]) continue;
vis[u] = 1;
for(int i = fir[u], v, w; i; i = E[i].nxt) {
v = E[i].v, w = E[i].w;
if(dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
q.push(make_pair(dis[v], v));
}
}
}
}
int main() {
n = read(), m = read(), k = read();
s = read() + 1, t = read() + 1;
for(int i = 1, a, b, c; i <= m; i++) {
a = read() + 1, b = read() + 1, c = read();
AddEdge(a, b, c);
AddEdge(b, a, c);
for(int j = 1; j <= k; j++) {
AddEdge(a + (j - 1) * n, b + j * n, 0);
AddEdge(b + (j - 1) * n, a + j * n, 0);
AddEdge(a + j * n, b + j * n, c);
AddEdge(b + j * n, a + j * n, c);
}
}
dijkstra(s);
ans = dis[0];
for(int i = 0; i <= k; i++)
ans = min(ans, dis[t + i * n]);
write(ans), putchar('\n');
return 0;
}
[NOI2010] 超级钢琴
小 Z 是一个小有名气的钢琴家,最近 C 博士送给了小 Z 一架超级钢琴,小 Z 希望能够用这架钢琴创作出世界上最美妙的音乐。
这架超级钢琴可以弹奏出 $n$ 个音符,编号为 $1$ 至 $n$。第 $i$ 个音符的美妙度为 $A_i$,其中 $A_i$ 可正可负。
一个“超级和弦”由若干个编号连续的音符组成,包含的音符个数不少于 $L$ 且不多于 $R$。我们定义超级和弦的美妙度为其包含的所有音符的美妙度之和。两个超级和弦被认为是相同的,当且仅当这两个超级和弦所包含的音符集合是相同的。
小 Z 决定创作一首由 $k$ 个超级和弦组成的乐曲,为了使得乐曲更加动听,小 Z 要求该乐曲由 $k$ 个不同的超级和弦组成。我们定义一首乐曲的美妙度为其所包含的所有超级和弦的美妙度之和。小 Z 想知道他能够创作出来的乐曲美妙度最大值是多少。
$-1000 \leq A_i \leq 1000$,$1 \leq L \leq R \leq n$
题解
对于左端点为 $o$ 的一段子区间,最优的答案为:
\[\max_{t\in [o+l-1,o+r - 1]} \sum_{i=o}^t A_i\]那么对于前缀和数组,确定左端点 $o$ 的情况下,只需求:
\[\max\limits_{t\in[o+l-1,o+r-1]} sum_t\]这个可以用 ST 表来 $\mathcal{O}(1)$ 解决。
然后枚举一遍左端点,将每一个可能的最大值加入堆里。从堆里取 $k$ 次最大值即可。
注意我们每一次取最大值后,要在除去这个最大值的位置后,重新把长度为 $[l, t]$ 和 $[t + 1, r]$ 的最大值加入堆里。
时间复杂度 $\mathcal{O}((n+k)\log n)$。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
inline ll read() {...}
inline void write(ll x) {...}
const int MAX_N = 5e5 + 10, MAX_LOG = 20;
int n, k, L, R;
ll ans, sum[MAX_N];
int log_2[MAX_N], st[MAX_N][MAX_LOG];
void init() {
log_2[1] = 0, log_2[2] = 1;
for(int i = 3; i <= n; i++)
log_2[i] = log_2[i >> 1] + 1;
for(int j = 1; j < MAX_LOG; j++)
for(int i = 1; i + (1 << j) - 1 <= n; i++) {
int x = st[i][j - 1], y = st[i + (1 << (j - 1))][j - 1];
st[i][j] = sum[x] > sum[y] ? x : y;
}
}
int query(int l, int r) {
int k = log_2[r - l + 1];
int x = st[l][k], y = st[r - (1 << k) + 1][k];
return sum[x] > sum[y] ? x : y;
}
struct node {
int o, l, r, t;
node() {}
node(int _o, int _l, int _r) :
o(_o), l(_l), r(_r), t(query(l, r)) {}
bool operator < (const node &T) const {
return sum[t] - sum[o - 1] < sum[T.t] - sum[T.o - 1];
}
};
priority_queue<node> q;
int main() {
n = read(), k = read(), L = read(), R = read();
for(int i = 1; i <= n; i++)
st[i][0] = i, sum[i] = sum[i - 1] + read();
init();
for(int i = 1; i <= n; i++)
if(i + L - 1 <= n) q.push(node(i, i + L - 1, min(i + R - 1, n)));
for(int i = 1; i <= k; i++) {
node tmp = q.top(); q.pop();
ans += sum[tmp.t] - sum[tmp.o - 1];
if(tmp.l != tmp.t) q.push(node(tmp.o, tmp.l, tmp.t - 1));
if(tmp.r != tmp.t) q.push(node(tmp.o, tmp.t + 1, tmp.r));
}
write(ans), putchar('\n');
return 0;
}
[LNOI2014]LCA
给出一个 $n$ 个节点的有根树(编号为 $0$ 到 $n-1$,根节点为 $0$)。
一个点的深度定义为这个节点到根的距离 $+1$。
设 $dep[i]$ 表示点i的深度,$LCA(i,j)$ 表示 $i$ 与 $j$ 的最近公共祖先。
有 $m$ 次询问,每次询问给出 $l\ r\ z$,求 $\sum_{i=l}^r dep[LCA(i,z)]$ 。
$1\le n\le 50000,1\le m\le 50000$。
题解
考虑差分,把询问拆成 $l - 1$ 和 $r$。离线下来按端点排序,对于每一个拆分的端点 $v$,在 $1$ 到 $u(u\le v)$ 的路径上加 $1$。所以当前的 $\sum dep =query(1, v)$。用线段树维护即可。
#include <bits/stdc++.h>
#define pb emplace_back
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
inline ll read() {...}
char buf[50];
inline void write(ll x) {...}
const int MAX_N = 5e4 + 10, MOD = 201314;
int d[MAX_N << 2], tag[MAX_N << 2];
int n, m, dfncnt, cnt;
int fa[MAX_N], dep[MAX_N], siz[MAX_N], hson[MAX_N], top[MAX_N], dfn[MAX_N];
vector<int> G[MAX_N];
pii ans[MAX_N];
struct que {
int r, z, belong; bool f;
que(int _r = 0, int _z = 0, int _belong = 0, bool _f = 0) :
r(_r), z(_z), belong(_belong), f(_f) {}
bool operator < (const que &t) const {return r < t.r;}
} q[MAX_N << 2];
void dfs1(int u) {
siz[u] = 1;
dep[u] = dep[fa[u]] + 1;
hson[u] = -1;
for(int v : G[u]) {
dfs1(v);
siz[u] += siz[v];
if(hson[u] == -1 || siz[hson[u]] < siz[v]) hson[u] = v;
}
}
void dfs2(int u, int tp) {
top[u] = tp;
dfn[u] = ++dfncnt;
if(hson[u] == -1) return;
dfs2(hson[u], tp);
for(int v : G[u])
if(v != hson[u]) dfs2(v, v);
}
inline int lc(int p) {return (p << 1);}
inline int rc(int p) {return (p << 1) | 1;}
inline int mid(int s, int t) {return s + ((t - s) >> 1);}
inline void pu(int p) {d[p] = (d[lc(p)] + d[rc(p)]) % MOD;}
inline void pd(int p, int s, int t) {
if(tag[p]) {
int m = mid(s, t);
(tag[lc(p)] += tag[p]) %= MOD, (tag[rc(p)] += tag[p]) %= MOD;
(d[lc(p)] += (m - s + 1) * tag[p] % MOD) %= MOD, (d[rc(p)] += (t - m) * tag[p] % MOD) %= MOD;
tag[p] = 0;
}
}
inline void update(int p, int s, int t, int l, int r) {
if(l <= s && t <= r) {
(d[p] += (t - s + 1) % MOD) %= MOD;
(tag[p] += 1) %= MOD;
return;
}
pd(p, s, t);
int m = mid(s, t);
if(l <= m) update(lc(p), s, m, l, r);
if(r > m) update(rc(p), m + 1, t, l, r);
pu(p);
}
inline int query(int p, int s, int t, int l, int r) {
if(l <= s && t <= r) return d[p];
pd(p, s, t);
int m = mid(s, t), ret = 0;
if(l <= m) (ret += query(lc(p), s, m, l, r)) %= MOD;
if(r > m) (ret += query(rc(p), m + 1, t, l, r)) %= MOD;
return ret;
}
inline void update_path(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
update(1, 1, n, dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
update(1, 1, n, dfn[x], dfn[y]);
}
inline int query_path(int x, int y) {
int ret = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
(ret += query(1, 1, n, dfn[top[x]], dfn[x])) %= MOD;
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
(ret += query(1, 1, n, dfn[x], dfn[y])) %= MOD;
return ret;
}
int main() {
n = read(), m = read();
for(int i = 2; i <= n; i++) {
fa[i] = read() + 1;
G[fa[i]].pb(i);
}
dfs1(1);
dfs2(1, 1);
for(int i = 1; i <= m; i++) {
int l = read() + 1, r = read() + 1, z = read() + 1;
q[++cnt] = que(l - 1, z, i, 0);
q[++cnt] = que(r, z, i, 1);
}
sort(q + 1, q + cnt + 1);
for(int i = 1, u = 0; i <= cnt; i++) {
while(u < q[i].r)
update_path(1, ++u);
int x = q[i].belong, res = query_path(1, q[i].z);
if(!q[i].f) ans[x].first = res;
else ans[x].second = res;
}
for(int i = 1; i <= m; i++)
write((ans[i].second - ans[i].first + MOD) % MOD), putchar('\n');
return 0;
}
♥