OI笔记 | 基础数据结构模板
单调栈
给出项数为 $n$ 的整数数列 $a_{1 \dots n}$。
定义函数 $f(i)$ 代表数列中第 $i$ 个元素之后第一个大于 $a_i$ 的元素的下标,即 $f(i)=\min_{i<j\leq n, a_j > a_i} {j}$。若不存在,则 $f(i)=0$。
试求出 $f(1\dots n)$。
题解
题意即:给定序列,问序列中每个数后面第一个比它大的数的下标。
从后往前遍历,维护一个单调递增栈。
遍历到一个位置时,弹出栈顶所有不大于它的数。弹出后栈顶剩下的数即为答案。这是因为若一个数既小又靠后,它就没有什么意义,不会影响正确性。
注意栈里面存的是下标。
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 3000006;
stack<int> s;
int a[MAX_N], ans[MAX_N];
inline int read() {...}
void write(int x) {...}
int main() {
int n = read();
for(int i = 1; i <= n; i++) a[i] = read();
for(int i = n; i >= 1; i--) {
while(!s.empty() && a[s.top()] <= a[i]) s.pop();
if(s.empty()) ans[i] = 0;
else ans[i] = s.top();
s.push(i);
}
for(int i = 1; i <= n; i++) write(ans[i]), putchar(' ');
return 0;
}
例题 积水面积
一组正整数,分别表示由正方体叠起的柱子的高度。若某高度值为 $x$,表示由 $x$ 个正立方的方块叠起(如下图,$0 \le x \le 5000$)。找出所有可能积水的地方(图中蓝色部分),统计它们可能积水的面积总和(计算的是图中的横截面积。一个立方体的位置,为一个单位面积)。
如图:柱子高度变化为 0 1 0 2 1 2 0 0 2 0。
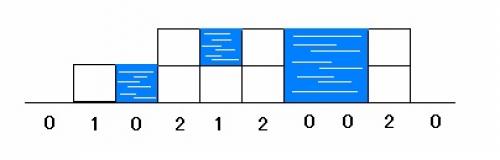
图中蓝色部分为积水面积,共有 $6$ 个单位面积积水。
题解
利用单调栈的思想:
正序遍历一遍,维护$lm_i = \max (a_1\dots a_i)$;
逆序遍历一遍,维护$rm_i = \max (a_i\dots a_n)$。
从而对于每一个位置$i$,它对答案的贡献为$\min(lm_i, rm_i) - a_i$。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 50003;
int a[MAX_N], lmax[MAX_N], rmax[MAX_N];
inline ll read() {...}
void write(ll x) {...}
int main() {
int n = read();
ll ans = 0;
for(int i = 1; i <= n; i++) a[i] = read();
for(int i = 1; i <= n; i++) lmax[i] = max(lmax[i - 1], a[i]);
for(int i = n; i >= 1; i--) rmax[i] = max(rmax[i + 1], a[i]);
for(int i = 1; i <= n; i++) ans += min(lmax[i], rmax[i]) - a[i];
write(ans);
return 0;
}
也可以用双指针法,节省空间复杂度。大致思路是:
对于位置$s$,先处理$a_s$是一段积水中较小的边的情况。向后遍历,期间将 $tmp$ 加上 $a_s - a_i$,直到找到第一个比它高的值,将答案加上 $tmp$ ,从这个位置继续向后遍历。
完成遍历后,再反向遍历处理 $a_s$ 是一段积水中较大的边的情况即可。
对顶堆
对顶堆是简单却好用的数据结构。以下内容来自 oi-wiki:
对顶堆由一个大根堆与一个小根堆组成,小根堆维护大值即前 $k$ 大的值(包含第 $k$ 个),大根堆维护小值即比第 $k$ 大数小的其他数。
这两个堆构成的数据结构支持以下操作:
-
维护:当小根堆的大小小于 $k$ 时,不断将大根堆堆顶元素取出并插入小根堆,直到小根堆的大小等于 $k$;当小根堆的大小大于 $k$ 时,不断将小根堆堆顶元素取出并插入大根堆,直到小根堆的大小等于 $k$;
-
插入元素:若插入的元素大于等于小根堆堆顶元素,则将其插入小根堆,否则将其插入大根堆,然后维护对顶堆;
-
查询第 $k$ 大元素:小根堆堆顶元素即为所求;
-
删除第 $k$ 大元素:删除小根堆堆顶元素,然后维护对顶堆;
-
$k$ 值 $+1/-1$:根据新的 $k$ 值直接维护对顶堆。
其中查询是 $O(1)$ 的,维护是 $O(\log n)$ 的。
中位数
要求每次插入一个数字,当序列中数字数量为奇数时,输出序列的中位数。
很裸的对顶堆题,只要令 $k=\frac{n + 1}{2}$ 即可。时间复杂度 $O(n\log n)$。
其实最开始做是用 vector + 二分做的, 时间复杂度是 $O(n^2 \log n)$,居然也能过,很离谱,可能是因为 STL 的常数太低了。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
priority_queue<int> p; // 大根堆
priority_queue<int, vector<int>, greater<int>> q;// 小根堆
inline ll read() {...}
inline void write(ll x) {...}
int main() {
int n = read();
int tmp = read(), mid = tmp;
write(mid); putchar('\n');
for(int i = 2; i <= n; i++) {
tmp = read();
if(tmp > mid) q.push(tmp);
else p.push(tmp);
if(i % 2) {
while(p.size() != q.size()) {
if(p.size() > q.size()) {
q.push(mid);
mid = p.top();
p.pop();
}
else {
p.push(mid);
mid = q.top();
q.pop();
}
}
write(mid);
putchar('\n');
}
}
return 0;
}
黑匣子
要求实现两种操作:向序列中插入一个数字 以及 查询序列中第 $k$ 小的值。每次查询时都让 $k+1$。
注意上面介绍的是维护第 $k$ 大的值,而这道题是维护第 $k$ 小的值。所以我们应该注意的是大根堆的大小与 $k$ 的关系,因为大根堆维护的才是小值。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 200005;
ll a[MAX_N];
priority_queue<ll> p;
priority_queue<ll, vector<ll>, greater<ll>> q;
inline ll read() {...}
inline void write(ll x) {...}
int main() {
int k = 0, o = 1, m = read(), n = read();
for(int i = 1; i <= m; i++) a[i] = read();
for(int i = 1; i <= n; i++) {
int t = read();
for(int x = o; x <= t; x++) {
if(q.empty() || a[x] < p.top()) p.push(a[x]);
else q.push(a[x]);
}
o = t + 1;
k++;
while(p.size() > k) q.push(p.top()), p.pop();
while(p.size() < k) p.push(q.top()), q.pop();
write(p.top());
putchar('\n');
}
return 0;
}
ST 表
能够 $O(1)$ 查 RMQ 的数据结构。
一维 ST 表
$O(n\log n)$ 建表。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 1e5 + 10, MAX_LOG = 18;
int st[MAX_N][MAX_LOG], log_2[MAX_N];
inline ll read() {...}
inline void write(ll x) {...}
void init() {
log_2[1] = 0; log_2[2] = 1;
for(int i = 3; i < MAX_N; i++) log_2[i] = log_2[i >> 1] + 1;
}
int main() {
init();
int n = read(), m = read();
for(int i = 1; i <= n; i++) st[i][0] = read();
for(int j = 1; j <= MAX_LOG; j++) {
for(int i = 1; i + (1 << (j - 1)) - 1 <= n; i++) {
st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
while(m--) {
int l = read(), r = read();
int x = log_2[r - l + 1];
write(max(st[l][x], st[r - (1 << x) + 1][x]));
putchar('\n');
}
return 0;
}
二维 ST 表

$O(ab \log (ab))$ 建表。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 1e3 + 10, MAX_LOG = 10;
int log_2[MAX_N], a, b, n, ans = 1e9;
struct ST {
int maxn, minn;
} st[MAX_N][MAX_N][MAX_LOG], k1, k2, k3, k4;
inline ll read() {...}
inline void write(ll x) {...}
inline void init() {
log_2[1] = 0, log_2[2] = 1;
for(int i = 3; i < MAX_N; i++) log_2[i] = log_2[i >> 1] + 1;
for(int k = 1; k <= MAX_LOG; k++) {
for(int i = 1; i + (1 << (k - 1)) - 1 <= a; i++) {
for(int j = 1; j + (1 << (k - 1)) - 1 <= b; j++) {
k1 = st[i][j][k - 1];
k2 = st[i][j + (1 << (k - 1))][k - 1];
k3 = st[i + (1 << (k - 1))][j][k - 1];
k4 = st[i + (1 << (k - 1))][j + (1 << (k - 1))][k - 1];
st[i][j][k].minn = min(k1.minn, min(k2.minn, min(k3.minn, k4.minn)));
st[i][j][k].maxn = max(k1.maxn, max(k2.maxn, max(k3.maxn, k4.maxn)));
}
}
}
}
inline int query(int i, int j, int k, bool type) {
int len = log_2[k];
k1 = st[i][j][len];
k2 = st[i][j + k - (1 << len)][len];
k3 = st[i + k - (1 << len)][j][len];
k4 = st[i + k - (1 << len)][j + k - (1 << len)][len];
if(type == 0) return min(k1.minn, min(k2.minn, min(k3.minn, k4.minn)));
else return max(k1.maxn, max(k2.maxn, max(k3.maxn, k4.maxn)));
}
int main() {
a = read(), b = read(), n = read();
for(int i = 1; i <= a; i++) for(int j = 1; j <= b; j++) st[i][j][0].minn = st[i][j][0].maxn = read();
init();
for(int i = 1; i <= a - n + 1; i++) for(int j = 1; j <= b - n + 1; j++) ans = min(ans, query(i, j, n, 1) - query(i, j, n, 0));
write(ans);
return 0;
}
线段树
模板1
维护一个线段树,支持对一个数列进行下面两种操作:
- 将某区间每一个数加上 $k$。
- 求出某区间每一个数的和。
$1 \le n, m \le {10}^5$, 其中 $n$ 为数列长度, $m$ 为操作次数。
题解
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 1e5+7;
ll a[MAX_N], d[MAX_N * 3], b[MAX_N * 3];
inline ll read() {...}
inline void write(ll x) {...}
void build_tree(int s, int t, int p) {
if(s == t) {d[p] = a[s]; return;}
int m = s + ((t - s) >> 1);
build_tree(s, m, p * 2), build_tree(m + 1, t, p * 2 + 1);
d[p] = d[p * 2] + d[p * 2 + 1];
}
void update(int l, int r, ll k, int s, int t, int p) {
if(l <= s && t <= r) {d[p] += (t - s + 1) * k; b[p] += k; return;}
int m = s + ((t - s) >> 1);
if(b[p] && s != t) {
d[p * 2] += (m - s + 1) * b[p], d[p * 2 + 1] += (t - m) * b[p];
b[p * 2] += b[p], b[p * 2 + 1] += b[p];
b[p] = 0;
}
if(l <= m) update(l, r, k, s, m, p * 2);
if(r > m) update(l, r, k, m + 1, t, p * 2 + 1);
d[p] = d[p * 2] + d[p * 2 + 1];
}
ll query(int l, int r, int s, int t, int p) {
if(l <= s && t <= r) return d[p];
int m = s + ((t - s) >> 1);
if(b[p] && s != t) {
d[p * 2] += (m - s + 1) * b[p], d[p * 2 + 1] += (t - m) * b[p];
b[p * 2] += b[p], b[p * 2 + 1] += b[p];
b[p] = 0;
}
ll sum = 0;
if(l <= m) sum += query(l, r, s, m, 2 * p);
if(r > m) sum += query(l, r, m + 1, t, 2 * p + 1);
return sum;
}
int main() {
int n = read(), m = read(), l, r, op;
ll k;
for(int i = 1; i <= n; i++) a[i] = read();
build_tree(1, n, 1);
for(int i = 1; i <= m; i++) {
op = read(), l = read(), r = read();
if(op == 1) {k = read(); update(l, r, k, 1, n, 1);}
else {write(query(l, r, 1, n, 1)); putchar('\n');}
}
return 0;
}
模板2
维护一个线段树,支持对一个数列进行下面两种操作:
- 将某区间每一个数乘上 $k$。
- 将某区间每一个数加上 $k$。
- 求出某区间每一个数的和。
$1 \le n, m \le {10}^5$, 其中 $n$ 为数列长度, $m$ 为操作次数。
题解
其实就是模板1加上一个乘法标记。对于区间的乘 $k$ 操作,我们把乘法标记和加法标记都乘上 $k$;而区间加只把加法标记加上 $k$。
注意在做 push_down 的时候往往是先做完乘在做加,这样能够满足乘法分配率。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 1e5+7;
ll a[MAX_N], d[MAX_N * 3], at[MAX_N * 3], mt[MAX_N * 3];
int n, m, MOD;
inline ll read() {...}
inline void write(ll x) {...}
void up(int p) {d[p] = (d[(p << 1)] + d[(p << 1) | 1]) % MOD;}
void build_tree(int s, int t, int p) {
at[p] = 0, mt[p] = 1;
if(s == t) {d[p] = a[s]; return;}
int m = s + ((t - s) >> 1);
build_tree(s, m, (p << 1));
build_tree(m + 1, t, (p << 1) | 1);
up(p);
}
void push_down(int p, int s, int t) {
int lc = (p << 1), rc = (p << 1) | 1;
int m = s + ((t - s) >> 1);
if(mt[p] != 1) {
mt[lc] = (mt[lc] * mt[p]) % MOD;
mt[rc] = (mt[rc] * mt[p]) % MOD;
at[lc] = (at[lc] * mt[p]) % MOD;
at[rc] = (at[rc] * mt[p]) % MOD;
d[lc] = (d[lc] * mt[p]) % MOD;
d[rc] = (d[rc] * mt[p]) % MOD;
mt[p] = 1;
}
if(at[p]) {
at[lc] = (at[lc] + at[p]) % MOD;
at[rc] = (at[rc] + at[p]) % MOD;
d[lc] = (d[lc] + at[p] * (m - s + 1)) % MOD;
d[rc] = (d[rc] + at[p] * (t - m)) % MOD;
at[p] = 0;
}
}
void ud_mul(int l, int r, int s, int t, int p, ll k) {
if(l <= s && t <= r) {
d[p] = (d[p] * k) % MOD;
mt[p] = (mt[p] * k) % MOD;
at[p] = (at[p] * k) % MOD;
return;
}
int m = s + ((t - s) >> 1);
if(s != t) push_down(p, s, t);
if(l <= m) ud_mul(l, r, s, m, (p << 1), k);
if(r > m) ud_mul(l, r, m + 1, t, (p << 1) | 1, k);
up(p);
}
void ud_add(int l, int r, int s, int t, int p, ll k) {
if(l <= s && t <= r) {
d[p] = (d[p] + k * (t - s + 1)) % MOD;
at[p] = (at[p] + k) % MOD;
return;
}
int m = s + ((t - s) >> 1);
if(s != t) push_down(p, s, t);
if(l <= m) ud_add(l, r, s, m, (p << 1), k);
if(r > m) ud_add(l, r, m + 1, t, (p << 1) | 1, k);
up(p);
}
ll query(int l, int r, int s, int t, int p) {
if(l <= s && t <= r) {return d[p];}
if(s != t) push_down(p, s, t);
int m = s + ((t - s) >> 1);
ll sum = 0;
if(l <= m) sum = (sum + query(l, r, s, m, (p << 1))) % MOD;
if(r > m) sum = (sum + query(l, r, m + 1, t, (p << 1) | 1)) % MOD;
return sum;
}
int main() {
n = read(), m = read(), MOD = read();
int x, y; ll k;
for(int i = 1; i <= n; i++) a[i] = read();
build_tree(1, n, 1);
for(int i = 1; i <= m; i++) {
int op = read(), x = read(), y = read();
if(op == 1) {k = read(); ud_mul(x, y, 1, n, 1, k);}
else if(op == 2) {k = read(); ud_add(x, y, 1, n, 1, k);}
else {write(query(x, y, 1, n, 1)); putchar('\n');}
}
return 0;
}
例题 守墓人
墓地分为主墓碑和次要墓碑, 主墓碑只能有 $1$ 个, 守墓人把他记为 $1$ 号, 而次要墓碑有 $n-1$ 个,守墓人将之编号为 $2,3\dots n$,所以构成了一个有 $n$ 个墓碑的墓地。每个墓地都有一个风水值。
守墓人会有几个操作:
-
将 $[l,r]$ 这个区间所有的墓碑的风水值增加 $k$
-
将主墓碑的风水值增加 $k$
-
将主墓碑的风水值减少 $k$
-
统计 $[l,r]$ 这个区间所有的墓碑的风水值之和
-
求主墓碑的风水值
数据范围:$1\leq n,f\leq 2 \times 10^5$,答案不超过 64 位整数。
题解
裸的线段树模板,主要是练习一遍写法。其实线段树模板还是很好背的。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 2e5 + 5;
ll a[MAX_N], d[MAX_N * 3], b[MAX_N * 3];
inline ll read() {...}
inline void write(ll x) {...}
inline int lc(int p) {return (p << 1);}
inline int rc(int p) {return (p << 1) | 1;}
inline void up(int p) {d[p] = d[lc(p)] + d[rc(p)];}
void push_down(int p, int s, int t) {
if(b[p]) {
int m = s + ((t - s) >> 1);
b[lc(p)] += b[p], b[rc(p)] += b[p];
d[lc(p)] += (m - s + 1) * b[p], d[rc(p)] += (t - m) * b[p];
b[p] = 0;
}
}
void build_tree(int s, int t, int p) {
if(s == t) {d[p] = a[s]; return;}
int m = s + ((t - s) >> 1);
build_tree(s, m, lc(p));
build_tree(m + 1, t, rc(p));
up(p);
}
void update(int l, int r, int s, int t, int p, ll k) {
if(l <= s && t <= r) {
d[p] += k * (t - s + 1);
b[p] += k;
return;
}
if(s != t) push_down(p, s, t);
int m = s + ((t - s) >> 1);
if(l <= m) update(l, r, s, m, lc(p), k);
if(r > m) update(l, r, m + 1, t, rc(p), k);
up(p);
}
ll query(int l, int r, int s, int t, int p) {
if(l <= s && t <= r) {return d[p];}
if(s != t) push_down(p, s, t);
int m = s + ((t - s) >> 1);
ll sum = 0;
if(l <= m) sum += query(l, r, s, m, lc(p));
if(r > m) sum += query(l, r, m + 1, t, rc(p));
return sum;
}
int main() {
int n = read(), f = read(), l, r;
ll k;
for(int i = 1; i <= n; i++) a[i] = read();
build_tree(1, n, 1);
for(int i = 1; i <= f; i++) {
int op = read();
if(op == 1) {
l = read(), r = read(), k = read();
if(l == 1) a[1] += k;
update(l, r, 1, n, 1, k);
}
else if(op == 2 || op == 3) {
k = read();
if(op == 3) k = -k;
update(1, 1, 1, n, 1, k);
a[1] += k;
}
else if(op == 4) {
l = read(), r = read();
write(query(l, r, 1, n, 1));
putchar('\n');
}
else {
write(a[1]);
putchar('\n');
}
}
return 0;
}
可持久化线段树
如题,你需要维护这样的一个长度为 $N$ 的数组,支持如下几种操作
-
在某个历史版本上修改某一个位置上的值
-
访问某个历史版本上的某一位置的值
此外,每进行一次操作(对于操作2,即为生成一个完全一样的版本,不作任何改动),就会生成一个新的版本。版本编号即为当前操作的编号(从1开始编号,版本0表示初始状态数组)
题解
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 1e6 + 10;
int a[MAX_N], root[MAX_N], n, m, tot;
struct node {
int lc, rc, val;
} d[MAX_N << 5];
inline ll read() {...}
inline void write(ll x) {...}
int mid(int s, int t) {return s + ((t - s) >> 1);}
int build_tree(int s, int t) {
int p = ++tot;
if(s == t) {
d[p].val = a[s];
return p;
}
int m = mid(s, t);
d[p].lc = build_tree(s, m);
d[p].rc = build_tree(m + 1, t);
return p;
}
int update(int s, int t, int pre, int pos, int val) {
int p = ++tot;
d[p] = d[pre];
if(s == t) {
d[p].val = val;
return p;
}
int m = mid(s, t);
if(pos <= m) d[p].lc = update(s, m, d[p].lc, pos, val);
else d[p].rc = update(m + 1, t, d[p].rc, pos, val);
return p;
}
int query(int s, int t, int p, int pos) {
if(s == t) return d[p].val;
int m = mid(s, t);
if(pos <= m) return query(s, m, d[p].lc, pos);
else return query(m + 1, t, d[p].rc, pos);
}
int main() {
n = read(), m = read();
for(int i = 1; i <= n; i++)
a[i] = read();
root[0] = build_tree(1, n);
for(int i = 1; i <= m; i++) {
int v = read(), op = read(), pos = read();
if(op == 1) {
int val = read();
root[i] = update(1, n, root[v], pos, val);
}
else {
write(query(1, n, root[v], pos)), putchar('\n');
root[i] = root[v];
}
}
return 0;
}
树状数组
$O(\log n)$ 查询前缀和/单点修改。
维护原数组的前缀和。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 5e5 + 10;
int a[MAX_N], tree[MAX_N], n, m;
inline ll read() {...}
inline void write(ll x) {...}
inline int lowbit(int x) {return x & -x;}
inline void update(int x, int k) {
while(x <= n) {
tree[x] += k;
x += lowbit(x);
}
}
inline int query(int x) {
int ret = 0;
while(x >= 1) {
ret += tree[x];
x -= lowbit(x);
}
return ret;
}
int main() {
n = read(), m = read();
for(int i = 1; i <= n; i++) {
int x = read();
update(i, x);
}
for(int i = 1; i <= m; i++) {
int op = read(), x = read(), k = read();
if(op == 1) update(x, k);
else write(query(k) - query(x - 1)), putchar('\n');
}
return 0;
}
维护差分数组的前缀和。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 5e5 + 10;
ll n, m, a[MAX_N], tree[MAX_N];
inline ll read() {...}
inline void write(ll x) {...}
inline ll lowbit(ll x) {return x & -x;}
inline void update(ll x, ll k) {for(ll i = x; i <= n; i += lowbit(i)) tree[i] += k;}
inline int query(ll x) {ll ret = 0; for(ll i = x; i >= 1; i -= lowbit(i)) ret += tree[i]; return ret;}
int main() {
n = read(), m = read();
for(int i = 1; i <= n; i++) a[i] = read();
for(int i = 1; i <= m; i++) {
int op = read();
if(op == 1) {
ll l = read(), r = read(), k = read();
update(l, k); update(r + 1, -k);
}
else {
ll x = read();
write(a[x] + query(x)); putchar('\n');
}
}
return 0;
}
数列分块
见 LINK。
柯朵莉树
珂朵莉树(Chtholly Tree),又名老司机树 ODT(Old Driver Tree),不是一种数据结构,而是基于数据随机的“颜色段均摊”提出的想法,可以效率较高地应用于有区间赋值操作的数据结构题。
对于区间加 add,区间赋值 assign,区间求和 sum 三种操作,可以证明数据随机情况下,用 set 实现的 ODT 的复杂度为 $O(n\log \log n)。$
下面给出一种实现,支持了 CF896C 要求的所有操作:
struct node {
ll l, r; mutable ll v;
node(ll l, ll r, ll v) : l(l), r(r), v(v) {}
inline bool operator < (const node &t) const {return l < t.l;}
};
typedef set<node>::iterator iter;
set<node> s;
iter split(ll x) {
if(x > n) return s.end();
iter it = --s.upper_bound(node{x, 0, 0});
if(it->l == x) return it;
ll l = it->l, r = it->r, v = it->v;
s.erase(it);
s.insert(node{l, x - 1, v});
return s.insert(node{x, r, v}).first;
}
void assign(ll l, ll r, ll v) {
iter ir = split(r + 1), il = split(l);
s.erase(il, ir);
s.insert(node{l, r, v});
}
void add(ll l, ll r, ll v) {
iter ir = split(r + 1), il = split(l);
for(; il != ir; il++)
il->v += v;
}
ll rnk(ll l, ll r, ll k) {
vector<pair<ll, int>> t;
iter ir = split(r + 1), il = split(l);
for(; il != ir; il++)
t.push_back({il->v, il->r - il->l + 1});
sort(t.begin(), t.end());
for(auto it = t.begin(); it != t.end(); it++) {
k -= it->second;
if(k <= 0) return it->first;
}
return -1;
}
ll qpow(ll a, ll b, ll p) {
ll ret = 1; a %= p;
while(b) {
if(b & 1) (ret *= a) %= p;
(a *= a) %= p;
b >>= 1;
}
return ret;
}
ll sum(ll l, ll r, ll x, ll p) {
iter ir = split(r + 1), il = split(l);
ll ret = 0;
for(; il != ir; il++)
(ret += (il->r - il->l + 1) * qpow(il->v, x, p) % p) %= p;
return ret;
}
注意的细节:
-
使用
mutable ll v来使得可以直接修改set中v的值。 -
必须先 split 右端点再 split 左端点。
笛卡尔树
给定一个 $1 \sim n$ 的排列 $p$,构建其笛卡尔树。
即构建一棵二叉树,满足:
- 每个节点的编号满足二叉搜索树的性质。
- 节点 $i$ 的权值为 $p_i$,每个节点的权值满足小根堆的性质。
使用 oi-wiki 上的写法。$O(n)$ 即可构建完成。
利用笛卡尔树可以求最大子矩形。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 1e7 + 10;
struct node {
int idx, val, par, lc, rc;
node(int idx = 0, int val = 0, int par = 0) : idx(idx), val(val), par(par) {lc = rc = 0;}
} tree[MAX_N];
inline ll read() {...}
inline void write(ll x) {...}
int main() {
int n = read();
for(int i = 1; i <= n; i++) {
int x = read(), k = i - 1;
tree[i] = node(i, x, 0);
while(tree[k].val > tree[i].val) k = tree[k].par;
tree[i].lc = tree[k].rc;
tree[k].rc = i;
tree[i].par = k;
tree[tree[i].lc].par = i;
}
ll ansl = 0, ansr = 0;
for(int i = 1; i <= n; i++)
ansl ^= 1ll * i * (tree[i].lc + 1), ansr ^= 1ll * i * (tree[i].rc + 1);
write(ansl), putchar(' '), write(ansr);
return 0;
}
- 上一篇 OI笔记 | 基础图论模板
- 下一篇 OI笔记 | 2022.11 做题记录(二)
♥