OI笔记 | 2022.10 做题记录(二)
洛谷上 10 月的提交记录:
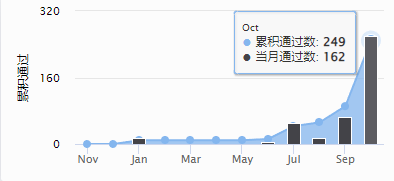
感觉确实停课期间刷了挺多题,不过水平提升没有很明显,继续努力。
- 电阻
- ABC小精灵
- Well played!
- 序列
- 最大正方形
- [CSP-J 2021] 网络连接
- [TJOI2009] 开关
- GSS4 - Can you answer these queries IV
- Can you answer these queries III
- [NOIP2017 提高组] 奶酪
- 出栈序列
- 关押罪犯
电阻
提供了无限个阻值为 $1$ 的电阻和电阻可以忽略不计的导线。
我们从一个阻值为 $1$ 的电阻开始,支持两种操作:
-
在原有的电路上串联一个阻值为 $1$ 的电阻。
-
在原有的电路上并联一个阻值为 $1$ 的电阻。
求最终需要的电阻(用分数 $A/B$ 表示)最少需要几个阻值为 $1$ 的电阻拼出来。
题解
设当前的阻值为 $A/B$,根据物理公式容易知道:
操作 $1$ 实际上把 $A/B$ 变为了 $(A+B)/B$;
操作 $2$ 实际上把 $A/B$ 变为了 $A/(A+B)$。
所以考虑逆推的过程即为把分子减去分母或把分母减去分子,所以容易想到用辗转相减法。考虑到这样的复杂度偏高,转化为等价的辗转相除法,直接使用 $f(A/B)=\lfloor A/B\rfloor + f(B, A\bmod B)$ 即可。
参考代码:
ll solve(ll a, ll b) {
if(b == 0) return 0;
return (a / b) + solve(b, a % b);
}
ABC小精灵
小精灵面前有两个只含有大写字母 A, B, C 的字符串 S1、S2。小精灵能识别的子串有: AA、BB、CC、ABAB、BCBC,共五个。在一次操作中,它能往字符串任意位置添加这其中的某个串,也能在字符串中找到并删除这其中的某个串。小精灵可以进行任意次操作,问它能否通过操作,将字符串 S1 变成字符串 S2。例如,S1=CABABA ,S2=CBCCCBCA,它的一种操作变换过程如下: CABABA->CA->CBCBCA->CBCCCBCA。
题解
赛时完全没有思路,然而结束时听隔壁讲了做法,感觉难度其实不大?还是自己的思路比较狭窄了吧。
考虑到 CBC 可以变成 ABA(CBC->ABABCBC->ABA),即居然可以无中生有,那么基本放弃使用 dp 了。根据隔壁的思路,此时我们可以猜想:要么答案中 C 与 A 等价,要么答案中 B 可以忽略。
注意到 AB->ABAA->ABABBA->BA,CB->CBBCBC->CCBC->BC。那么 B 的位置与答案无关,不妨视为全部移到字符串的开头。在这之后如果两个串中删掉所有连续两个字母后相等,即可以变换。
代码实现方面可以统计 B 的数量,并把剩下非一对的 A 或 C 推入另外的字符串 m 和 n。那么当 $cnt_1\equiv cnt_2(\bmod 2)$ 且 m == n 时可以变换成功。
参考代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {...}
inline void write(ll x) {...}
int main() {
int T = read();
while(T--) {
string s1, s2, m = "", n = "";
int cnt1 = 0, cnt2 = 0;
cin >> s1 >> s2;
for(int i = 0; i < s1.size(); i++) {
if(s1[i] != 'B') {
if(m == "" || s1[i] != m[m.size() - 1]) m.push_back(s1[i]);
else m.pop_back();
}
else cnt1++;
}
for(int i = 0; i < s2.size(); i++) {
if(s2[i] != 'B') {
if(n == "" || s2[i] != n[n.size() - 1]) n.push_back(s2[i]);
else n.pop_back();
}
else cnt2++;
}
if(m == n && cnt1 % 2 == cnt2 % 2) printf("YES\n");
else printf("NO\n");
}
return 0;
}
Well played!
小 Y 最近沉迷于一款打怪游戏《赛某号》。现在,他正在参加赛某号的春季联赛。
他有 $n$ 只精灵。每只精灵都有对应的生命值 $hp_i$ 和攻击值 $d_i$。在比赛过程中,小 Y 可以借助巴拉拉小魔仙之力,说出这两种咒语:
1、“乌卡拉!血量!加倍!“意即将当前精灵的生命值加倍。
2、“乌卡拉!生命之力!”意即将当前精灵的生命值赋给当前精灵的攻击值。(使得 $d_i=hp_i$)
小 Y 当然不能无限使用这两种咒语。在一局游戏中,他可以使用第一种咒语 $a$ 次,第二次咒语 $b$ 次。由于小 Y 购买了超级 Nono,所以这两种咒语都可以被多次用在同一精灵身上,且咒语的使用顺序没有限制。小 Y 可以不用完所有的咒语。
小 Y 非常希望通过使用这些咒语使得自己的精灵战斗群的攻击值达到最大。现在,小 Y 想知道这个最大值。
题解
考虑到对于咒语 1, 可以贪心地把它加到同一个精灵上。但注意这也需要用一次咒语 2。
对于咒语 2,我们按替换掉的增加量排序,施加到前 $b$ 个上面。
参考代码:
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 2e5 + 10;
typedef long long ll;
typedef pair<int, int> pii;
pii a[MAX_N];
bool cmp(pii x, pii y) {return x.first - x.second > y.first - y.second;}
inline ll read() {...}
inline void write(ll x) {...}
int main() {
int n = read(), t = read(), b = read();
ll sum = 0;
for(int i = 1; i <= n; i++) a[i].first = read(), a[i].second = read();
sort(a + 1, a + n + 1, cmp);
for(int i = 1; i <= b; i++) sum += max(a[i].first, a[i].second);
for(int i = b + 1; i <= n; i++) sum += a[i].second;
ll ans = sum;
if(b) {
for(int i = 1; i <= b; i++) ans = max(ans, sum + a[i].first * (1ll << t) - max(a[i].first, a[i].second));
sum = sum - max(a[b].second, a[b].first) + a[b].second;
// 留一次咒语 2 给后面的 [b+1, n]
for(int i = b + 1; i <= n; i++) ans = max(ans, sum + a[i].first * (1ll << t) - a[i].second);
}
write(ans);
}
序列
现有 $n$ 个不超过 $10^6$ 的合数,每个均可表示为 $p\times q$ ( $p,q$ 为两个互异素数)。若 $a=p_1\times q_1(p_1<q_1)$, $b=p_2\times q_2(p_2<q_2)$,当且仅当 $q_1=p_2$ 时 $b$ 能接在 $a$ 后面。 请问从给定的这 $n$ 个数中选数接龙,最长可以形成一个包含多少数的接龙序列?
题解
我们以质数为点,若 $x=p\times q$,则加一条有向边 $p\to q$,显然去重后会建出一个 DAG。对这个 DAG 进行拓扑排序,顺带做最长路的 dp 即可。
可以视为 DAG 上 dp 的模板。代码实现方面写了一些注释。
参考代码:
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 1000010, MAX_T = 100010, INF = (1 << 30);
typedef long long ll;
typedef pair<int, int> pii;
struct Edge {int u, v;};
bool p[MAX_N];
int dp[MAX_T], in[MAX_T], n, num, ans;
pii pt[MAX_T];
vector<int> primes, f, G[MAX_T];
vector<Edge> edges;
inline ll read() {...}
inline void write(ll x) {...}
void AddEdge(int u, int v) {
edges.push_back({u, v});
G[u].push_back(edges.size() - 1); // G 里存的都是边的编号
in[v]++;
}
void init(int mx) {
// 埃氏筛法
for(int i = 2; i <= mx; i++) {
if(!p[i]) primes.push_back(i);
for(int j = 1; j * i <= mx; j++) p[i * j] = 1;
}
}
void topo() {
// 拓扑排序
queue<int> q;
for(int i = 0; i < num; i++) {
if(in[i] == 0) {
dp[i] = 0;
q.push(i);
}
else dp[i] = -INF;
}
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = 0; i < G[u].size(); i++) {
int v = edges[G[u][i]].v;
dp[v] = max(dp[v], dp[u] + 1); // 最长路 dp 的状态转移方程
ans = max(ans, dp[v]);
if(--in[v] == 0) q.push(v);
}
}
}
int main() {
n = read();
init(MAX_N);
for(int i = 1; i <= n; i++) {
int x = read();
for(int k = 0; k < primes.size(); k++) {
if(x % primes[k] == 0) {
int m = primes[k], n = x / primes[k];
pt[i].first = m, pt[i].second = n; // m -> n 有一条边
f.push_back(m), f.push_back(n); // 将每个点单独存入 vector,便于排序去重离散化
break;
}
}
}
sort(f.begin(), f.end());
auto ed = unique(f.begin(), f.end()); // 注意 vector 的 unique 返回迭代器
num = ed - f.begin(); // 有效点的数量
for(int i = 1; i <= n; i++) {
int u = lower_bound(f.begin(), ed, pt[i].first) - f.begin();
int v = lower_bound(f.begin(), ed, pt[i].second) - f.begin();
// 离散化, u 和 v 是这个质数在 f 中的编号
AddEdge(u, v);
}
topo();
write(ans);
return 0;
}
最大正方形
在一个 $n\times m$ 的只包含 $0$ 和 $1$ 的矩阵里找出一个不包含 $0$ 的最大正方形,输出边长。$(1\leq n,m\leq 100)$
题解
我们预处理出矩阵的二维前缀和,从大到小枚举正方形边长 $l$ 与 正方形的左上角下标 $(i,j)$,每次可以 $O(1)$ 计算出正方形内的和,若它等于 $l^2$ 即匹配出合法的正方形了。最差时间复杂度 $O(n^3)$。
参考代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 105;
int f[MAX_N][MAX_N];
inline ll read() {...}
inline void write(ll x) {...}
int main() {
int n = read(), m = read();
for(int i = 1; i <= n; i++) {
int sum = 0;
for(int j = 1; j <= m; j++) {
sum += read();
f[i][j] = f[i - 1][j] + sum;
}
}
int l = min(n, m) + 1;
while(l--) {
for(int i = 1; i + l - 1 <= n; i++) {
for(int j = 1; j + l - 1 <= m; j++) {
if(f[i + l - 1][j + l - 1] - f[i - 1][j + l - 1] - f[i + l - 1][j - 1] + f[i - 1][j - 1] == l * l) {
write(l);
return 0;
}
}
}
}
write(0);
return 0;
}
[CSP-J 2021] 网络连接
有 $n$ 台编号为 $1 \sim n$ 的计算机,分为服务机(Server)和客户机(Client)两种。服务机负责建立连接,客户机负责加入连接。进行相应操作时,每个计算机需要提供一个地址串。
一个符合规范的地址串应当具有以下特征:
- 必须形如
a.b.c.d:e的格式,其中 $a, b, c, d, e$ 均为非负整数; - $0 \le a, b, c, d \le 255$,$0 \le e \le 65535$;
- $a, b, c, d, e$ 均不能含有多余的前导 $0$。
你要在给出每台计算机的类型以及地址串之后,判断这台计算机的连接情况。
如果第 $i$ 台计算机为服务机,则:
- 如果其提供符合规范的地址串且成功建立连接,输出字符串
OK。 - 如果其提供符合规范的地址串,但由于先前有相同地址串的服务机而无法成功建立连接,输出字符串
FAIL。 - 如果其提供的地址串不是符合规范的地址串,输出字符串
ERR。
如果第 $i$ 台计算机为客户机,则:
- 如果其提供符合规范的地址串且成功加入连接,输出一个正整数表示这台客户机连接到的服务机的编号。
- 如果其提供符合规范的地址串,但无法成功加入连接时,输出字符串
FAIL。 - 如果其提供的地址串不是符合规范的地址串,输出字符串
ERR。
题解
比较简单的大模拟,只要大样例过了基本上就能 AC。
难点主要是在判断地址串是否合法上,容易遗漏一些情况。所以可以不断测大样例, windows 下用 fc.exe 来对比而找到遗漏的情况,加以改正即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
map<string, int> mp;
inline ll read() {...}
inline void write(ll x) {...}
bool check(string ad) {
int cnt1 = 0, cnt2 = 0, i = 0;
for(i = 0; i < ad.size(); i++) {
if(ad[i] == '.') cnt1++;
if(ad[i] == ':') cnt2++;
}
if(cnt1 != 3 || cnt2 != 1) return false; // '.'和':' 的数量不能多不能少
i = 0;
string tmp;
for(int k = 1; k <= 4; k++) {
while((k == 4) ? ad[i] != ':' : ad[i] != '.') {
tmp += ad[i];
if(!isdigit(ad[i])) return false;
i++;
} // 到 '.' 或 ':' 暂停查找,判断当前是否合法
if(!tmp.size() || (tmp.size() >= 2 && tmp[0] == '0')) return false;
if(tmp.size() > 3 || (tmp.size() == 3 && tmp > "255")) return false;
tmp = ""; i++;
}
for(i; i < ad.size(); i++) {
tmp += ad[i];
if(!isdigit(ad[i])) return false;
}
if(!tmp.size() || (tmp.size() >= 2 && tmp[0] == '0')) return false;
if(tmp.size() > 5 || (tmp.size() == 5 && tmp > "65535")) return false;
return true;
}
int main() {
int n = read();
for(int i = 1; i <= n; i++) {
string op, ad;
cin >> op >> ad;
bool type = (op[0] == 'S');
if(!check(ad)) printf("ERR\n");
else {
if(type) {
if(mp[ad]) printf("FAIL\n");
else printf("OK\n"), mp[ad] = i;
}
else {
if(mp[ad]) write(mp[ad]), putchar('\n');
else printf("FAIL\n");
}
}
}
return 0;
}
[TJOI2009] 开关
现有 $n$ 盏灯排成一排,从左到右依次编号为:$1$,$2$,……,$n$。然后依次执行 $m$ 项操作。
操作分为两种:
- 指定一个区间 $[a,b]$,然后改变编号在这个区间内的灯的状态(把开着的灯关上,关着的灯打开);
- 指定一个区间 $[a,b]$,要求你输出这个区间内有多少盏灯是打开的。
灯在初始时都是关着的。
题解
看上去就是线段树的板子。简单来说就是支持 区间修改异或 和 区间求和。于是我们的线段树维护区间内亮灯的灯数,懒惰标记记录这个节点需不需要修改,下传时让 $b[lc(p)] \oplus 1, b[rc(p)] \oplus 1$ 即可。
修改时,这个节点上的 亮灯的灯数 变为 原来不亮的灯数,即 (区间的长度 - 亮灯的灯数)。这样就相当于取反了。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 2e6 + 10;
ll d[MAX_N], b[MAX_N];
inline ll read() {...}
inline void write(ll x) {...}
inline ll lc(ll p) {return (p << 1);}
inline ll rc(ll p) {return (p << 1) | 1;}
inline void pu(ll p) {d[p] = d[lc(p)] + d[rc(p)];}
inline void pd(ll p, ll s, ll t) {
if(b[p]) {
ll mid = s + ((t - s) >> 1);
b[lc(p)] ^= 1, b[rc(p)] ^= 1;
d[lc(p)] = (mid - s + 1) - d[lc(p)], d[rc(p)] = (t - mid) - d[rc(p)];
b[p] = 0;
}
}
void update(ll s, ll t, ll l, ll r, ll p) {
if(l <= s && t <= r) {
b[p] ^= 1;
d[p] = (t - s + 1) - d[p];
return;
}
pd(p, s, t);
ll mid = s + ((t - s) >> 1);
if(l <= mid) update(s, mid, l, r, lc(p));
if(r > mid) update(mid + 1, t, l, r, rc(p));
pu(p);
}
ll query(ll s, ll t, ll l, ll r, ll p) {
if(l <= s && t <= r) return d[p];
pd(p, s, t);
ll mid = s + ((t - s) >> 1), ret = 0;
if(l <= mid) ret += query(s, mid, l, r, lc(p));
if(r > mid) ret += query(mid + 1, t, l, r, rc(p));
return ret;
}
int main() {
int n = read(), m = read();
for(int i = 1; i <= m; i++) {
ll op = read(), l = read(), r = read();
if(op) write(query(1, n, l, r, 1)), putchar('\n');
else update(1, n, l, r, 1);
}
return 0;
}
GSS4 - Can you answer these queries IV
有 $n$ 个数,保证 $\sum a_i \leq 10^{18}$。
你需要支持两种操作:
-
0 x y:把区间 $[x,y]$ 内的每个数开方,下取整。 -
1 x y:询问区间 $[x,y]$ 的每个数的和。
题解
用线段树来维护。注意到开方开多了总是会变成 $1$ 的(六七次就足够了),如果整个区间都是 $1$,就不用再递归下去了,否则暴力递归下去单点修改。
具体来说,用 b[p] 来储存这个节点代表的区间内最大的数,当且仅当 b[p] > 1 时递归下去修改。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 5e5 + 10;
ll a[MAX_N], d[MAX_N], b[MAX_N];
inline ll read() {...}
inline void write(ll x) {...}
inline int lc(int p) {return (p << 1);}
inline int rc(int p) {return (p << 1) | 1;}
inline void pu(int p) {
b[p] = max(b[lc(p)], b[rc(p)]);
d[p] = d[lc(p)] + d[rc(p)];
}
void build_tree(int s, int t, int p) {
if(s == t) {b[p] = d[p] = a[s]; return;}
int mid = s + ((t - s) >> 1);
build_tree(s, mid, lc(p));
build_tree(mid + 1, t, rc(p));
pu(p);
}
void update(int s, int t, int p, int l, int r) {
if(s == t) {b[p] = d[p] = sqrt(d[p]); return;}
int mid = s + ((t - s) >> 1);
if(l <= mid && b[lc(p)] > 1) update(s, mid, lc(p), l, r);
if(r > mid && b[rc(p)] > 1) update(mid + 1, t, rc(p), l, r);
pu(p);
}
ll query(int s, int t, int p, int l, int r) {
if(l <= s && t <= r) {return d[p];}
int mid = s + ((t - s) >> 1);
ll ret = 0;
if(l <= mid) ret += query(s, mid, lc(p), l, r);
if(r > mid) ret += query(mid + 1, t, rc(p), l, r);
return ret;
}
int main() {
int n, ks = 0;
while(cin >> n) {
memset(d, 0, sizeof(d));
memset(b, 0, sizeof(b));
memset(a, 0, sizeof(a));
printf("Case #%d:\n", ++ks);
for(int i = 1; i <= n; i++) a[i] = read();
build_tree(1, n, 1);
int m = read();
while(m--) {
int k = read(), l = read(), r = read();
if(l > r) swap(l, r);
if(!k) update(1, n, 1, l, r);
else write(query(1, n, 1, l, r)), putchar('\n');
}
putchar('\n');
}
return 0;
}
Can you answer these queries III
$n$ 个数,$q$ 次操作
操作0 x y把$A_x$ 修改为$y$
操作1 l r询问区间$[l, r]$ 的最大子段和
题解
这道题我们要在线段树每个节点维护的信息比较多。包括区间最大子段和 $val$,从区间左端向右的最大子段和 $lmax$,从区间右端向左的最大子段和 $rmax$,以及区间和 $sum$。
于是在 push-up 的时候可以推出:
$sum=lc.sum + rc.sum$;
$lmax = \max(lc.lmax, lc.sum+rc.lmax)$;
$rmax = \max(rc.rmax, rc.sum+lc.rmax)$;
$val = \max(lc.val, rc.val, lc.rmax + rc.lmax)。$
由于询问时有可能要把区间切成两块 $[l,mid]$ 和 $[mid,r]$,我们让函数的返回值为 node,便于处理。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 50005;
int a[MAX_N];
struct node {
int val, lmax, rmax, sum;
} d[MAX_N * 4];
inline ll read() {...}
inline void write(ll x) {...}
inline int lc(int p) {return (p << 1);}
inline int rc(int p) {return (p << 1) | 1;}
inline int mid(int s, int t) {return s + ((t - s) >> 1);}
inline void pu(int p) {
d[p].sum = d[lc(p)].sum + d[rc(p)].sum;
d[p].lmax = max(d[lc(p)].lmax, d[lc(p)].sum + d[rc(p)].lmax);
d[p].rmax = max(d[rc(p)].rmax, d[rc(p)].sum + d[lc(p)].rmax);
d[p].val = max(d[lc(p)].val, d[rc(p)].val);
d[p].val = max(d[p].val, d[lc(p)].rmax + d[rc(p)].lmax);
}
void build_tree(int s, int t, int p) {
if(s == t) {
d[p].val = d[p].lmax = d[p].rmax = d[p].sum = a[s];
return;
}
int m = mid(s, t);
build_tree(s, m, lc(p));
build_tree(m + 1, t, rc(p));
pu(p);
}
void update(int s, int t, int p, int x, int k) {
if(s == t) {
d[p].val = d[p].lmax = d[p].rmax = d[p].sum = k;
return;
}
int m = mid(s, t);
if(x <= m) update(s, m, lc(p), x, k);
else update(m + 1, t, rc(p), x, k);
pu(p);
}
node query(int s, int t, int p, int l, int r) {
if(l <= s && t <= r) return d[p];
int m = mid(s, t);
if(r <= m) return query(s, m, lc(p), l, r);
if(l > m) return query(m + 1, t, rc(p), l, r);
node ret, L = query(s, m, lc(p), l, m), R = query(m + 1, t, rc(p), m + 1, r);
ret.sum = L.sum + R.sum;
ret.lmax = max(L.lmax, L.sum + R.lmax);
ret.rmax = max(R.rmax, R.sum + L.rmax);
ret.val = max(L.val, R.val);
ret.val = max(ret.val, L.rmax + R.lmax);
return ret;
}
int main() {
int n = read();
for(int i = 1; i <= n; i++) a[i] = read();
build_tree(1, n, 1);
int q = read();
while(q--) {
int op = read(), x = read(), y = read();
if(!op) update(1, n, 1, x, y);
else write(query(1, n, 1, x, y).val), putchar('\n');
}
return 0;
}
[NOIP2017 提高组] 奶酪
空间直角坐标系中有一块奶酪,它的长宽的上表面为平面 $z = h$,下表面为平面 $z = 0$。
奶酪中有 $n$ 个球形空洞,它们的半径均为 $r$。如果存在空洞与下表面相切或相交,则它与下表面连通。如果存在空洞与上表面相切或相交,则它与上表面连通。如果两个空洞是相切或相交的,则它们连通。
给出每个空洞的球心坐标 $(x_i, y_i,z_i)$,询问下表面和上表面是否连通。
数据范围:$1 \le n \le 1\times 10^3$,$1 \le h , r \le 10^9$,$T \le 20$,坐标的绝对值不超过 $10^9$。
题解
用并查集维护即可。将上表面和下表面存到虚拟节点 $n + 1$ 和 $n + 2$ 中,最终它们在同一个集合里即为连通。
时间复杂度: $O(Tn^2)$。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int MAX_N = 1e3 + 10;
ll f[MAX_N], n, h, r;
struct point {
ll x, y, z;
} a[MAX_N];
inline ll read() {...}
inline void write(ll x) {...}
inline bool isUnion(point m, point n) {
ll x = m.x, y = m.y, z = m.z, X = n.x, Y = n.y, Z = n.z;
ull dis = (x - X) * (x - X) + (y - Y) * (y - Y) + (z - Z) * (z - Z);
ull rr = 4 * r * r;
return dis <= rr;
}
inline ll find(ll x) {
if(f[x] == x) return x;
return f[x] = find(f[x]);
}
inline void Union(ll i, ll j) {f[find(i)] = find(j);}
int main() {
ll T = read();
while(T--) {
n = read(), h = read(), r = read();
for(ll i = 1; i <= n + 2; i++) f[i] = i;
for(ll i = 1; i <= n; i++) {
a[i].x = read(), a[i].y = read(), a[i].z = read();
if(a[i].z - r <= 0) Union(i, n + 1);
if(a[i].z + r >= h) Union(i, n + 2);
for(ll j = 1; j < i; j++) {
if(find(i) == find(j)) continue;
if(isUnion(a[i], a[j])) Union(i, j);
}
}
printf("%s\n", find(n + 1) == find(n + 2) ? "Yes" : "No");
}
return 0;
}
出栈序列
给定一个 $n$ 个元素组成的序列,将其中的元素按顺序压入一个大小为 $c$ 的栈 $s$ 并弹出,输出字典序最小的出栈序列。
题解
依次考虑每一步怎么得出一个答案。出栈的这个数,可能是入栈几个数再出栈,也可能是直接出栈。
我们维护两个指针 $l, r$,使得区间 $[l, r]$ 为当前可能进栈的数,那么显然有 $r = \min(l + c - s.size + 1, n)$。
每次找出 $[l,r]$ 中最小的数,设它的下标为 $k$。如果它比栈顶元素小,我们进栈 $[l, k-1]$ 的所有元素,输出 $a_k$,然后让 $l$ 指向 $k + 1$。否则,我们出栈栈顶元素。
找出最小的数可以用各种方式,包括单调队列、ST 表、线段树等。
使用 ST 表的参考代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 1e5 + 10, MAX_LOG = 15;
stack<int> s;
int a[MAX_N], st[MAX_N][MAX_LOG], log_2[MAX_N], n, c;
inline ll read() {...}
inline void write(ll x) {...}
void init() {
log_2[1] = 0, log_2[2] = 1;
for(int i = 3; i < MAX_N; i++) log_2[i] = log_2[i >> 1] + 1;
for(int i = 1; i <= n; i++) st[i][0] = a[i];
for(int j = 1; j <= MAX_LOG; j++) {
for(int i = 1; i + (1 << (j - 1)) - 1 <= n; i++) {
st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
}
int Min(int l, int r) {
int len = log_2[r - l + 1];
return min(st[l][len], st[r - (1 << len) + 1][len]);
}
int main() {
n = read(), c = read();
for(int i = 1; i <= n; i++) a[i] = read();
init();
int l = 1, r = c;
while(l <= n) {
r = min(l + c - (int)s.size() - 1, n);
int mx = Min(l, r);
if(s.empty() || mx < s.top()) {
int k;
for(k = l; a[k] != mx; k++) s.push(a[k]);
write(mx), putchar(' ');
l = k + 1;
}
else {
write(s.top()), putchar(' ');
s.pop();
}
}
while(!s.empty()) {
write(s.top()), putchar(' ');
s.pop();
}
return 0;
}
关押罪犯
有两座监狱,需要关押 $N$ 名罪犯,编号分别为 $1-N$。给出 $M$ 个关系,每个关系 $(u,v,c)$ 表示罪犯 $u$ 和 罪犯 $v$ 如果被关押在同一监狱,会造成影响力为 $c$ 的冲突事件。
分配这 $N$ 名罪犯到两个监狱,使得所有冲突事件的影响力的最大值最小,求出这个最小值。
题解
考虑将关系按影响力排序,我们优先解决影响力大的事件。用并查集维护当前罪犯分配的情况。
如果处理到此处, $u_i$ 和 $v_i$ 已经在同一个监狱,那么无法再解决了,直接输出这个影响力。否则,将 $u$ 分配到 $v$ 的敌人所关押的监狱,将 $v$ 分配到 $u$ 的敌人所关押的监狱。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 1e5 + 10, N = 20005;
struct edge {
int u, v, c;
bool operator < (const edge &t) const {return c > t.c;}
} E[MAX_N];
int f[MAX_N], d[MAX_N];
inline ll read() {...}
inline void write(ll x) {...}
int find(int x) {
if(f[x] == x) return x;
return f[x] = find(f[x]);
}
int main() {
int n = read(), m = read();
for(int i = 1; i <= n; i++) f[i] = i;
for(int i = 1; i <= m; i++) {
int u = read(), v = read(), c = read();
E[i] = {u, v, c};
}
sort(E + 1, E + m + 1);
for(int i = 1; i <= m + 1; i++) {
int u = E[i].u, v = E[i].v;
int fu = find(u), fv = find(v);
if(fu == fv) {
write(E[i].c);
break;
}
else {
if(!d[u]) d[u] = v;
else f[fv] = find(d[u]);
if(!d[v]) d[v] = u;
else f[fu] = find(d[v]);
}
}
return 0;
}
♥