暑期笔记 | OI中的基础数学 (数论和组合等)
Latex敲得好累…数学还真是不好学阿(感叹)
Fibonacci数列
递推式:$f[1]=f[2]=1, f[n]=f[n-1]+f[n-2] (n\geq 3)$
性质:
- 相邻两项的最大公约数为$1$(可用辗转相除法证明)
- 当$n\rightarrow +\infty$时,$f[n-1]:f[n]\rightarrow 0.6180339…$(黄金分割数)
- 由于$Fibonacci$数列是指数增长的,可知从$1,2,3,…,N$中,$Fibonacci$数的数量级为$\log N$
质数
除了$1$与本身之外不再有其他因数的数是质数。
若$\exists\ i \in (1,x)$,使得$i\mid x$,则整数$x$是合数。
质数的判断
试除法
bool isPrime(int x) {
if(x<2) return false;
for(int i=2;i*i<=x;i++) if(x%i==0) return false;
return true;
}
时间复杂度:$O(\sqrt n)$
埃氏筛法
vector<int> primes;
bool vis[MAX_N];
//获取区间 [2, MAX_N] 中的所有质数
void get_primes(){
for(int i = 2; i <= MAX_N; i++){
if(vis[i]) continue;
primes.push_back(i);
for(int j = i; j <= n/i; j++) vis[i*j] = 1;
}
}
埃氏筛法:遍历$[2, n]$的每一个数,把它的所有倍数做一个标记。如果遍历到了这个数,且这个数还没有被标记过,则这个数是一个质数。
时间复杂度:$O(n\log n)$
分解质因数
每个大等于$2$的正整数一定可以表示成几个质数相乘,并仅有一种这样的因数分解。(唯一分解定理)
\[x = p_1^{k_1} \times p_2^{k_2}\times p_3^{k_3}\times .....p_n^{k_n}\]可以估算有关数的数量级:$1 \le k, n < \log_2x$,所以大部分情况可以大胆枚举。
容易证明:在所有的质因数$p_i$中,最多有一个大于$\sqrt x$的质因数。这是因为若有两个或以上这样的质因数,那么他们相乘必然大于$x$。这意味着我们在分解质因数时只需要从$2$枚举到$\sqrt x$。
int n; // 对n分解质因数
for(int i=2;i*i<=n;i++){
while(n%i==0){
n /= i;
cout << i << endl; // 输出质因数
}
}
if(n>1) cout << n; // 处理完所有小于sqrt(n)的质因数后剩下的质因数
以上分解质因数的代码是$O(\sqrt n)$的。
int k(int n){
int cnt=0;
for(int i=2;i*i<=n;i++){
if(n%i==0) cnt++;
while(n%i==0) n/=i;
}
if(n>1) cnt++;
return cnt;
}
以上函数返回$n$中不同质因数的个数。
约数个数d(x)
引理1:
若$x$和$y$互质,则$x$的因数和$y$的因数都不同,从$x$的因数和$y$的因数中任选一个出来相乘,都能得到$x\times y$的一个因数。所以根据乘法原理,我们有:
\(d(x\times y)=d(x)\times d(y)\).
引理2:
考虑质数的幂$p^k$,它的约数为$p^0,\ p^1,\ …p^{k}$。所以$d(p^k)=k+1$。
计算d(x)
根据引理1,2 , 即可得出:
\[d(x) = d(p_1^{k_1} \times p_2^{k_2}\times ...p_n^{k_n})\\=d(p_1^{k_1})\times d(p_2^{k_2})\times ...d(p_n^{k_n})\\=(k_1+1)(k_2+1)...(k_n+1)\]即 $d(x)=\prod\limits_{i=1}^n(k_i+1)$ ($k_i$为第$i$个质因数的次数)
所以只需分别求出各个质因数的幂次即可,时间复杂度$O(\sqrt n)$。
int d(int x){
int ans=1, cpower;
for(int i=2;i*i<=x;i++){
cpower=0; //第i个质因数的次数
while(x%i==0){
x/=i; //试除所有可能的质因数
cpower++;
}
ans*=cpower+1; //连乘
}
if(x>1) ans*=2; //此句解释见分解质因数的代码
return ans;
}
习题
题面
给出数字$n$,求有多少组解满足:
\[\frac{1}{x} + \frac{1}{y} = \frac{1}{n}(1\le x \le y)\]题解
\[\frac{1}{x} + \frac{1}{y} = \frac{1}{n}\] \[\iff xy-yn-xn=0\] \[\iff (x-n)(y-n)=n^2\]那么每一对$(x-n, y-n)$对应唯一的原方程的解$(x, y)$。
从而只需求$n^2$能被分成几种两数相乘的形式即可,可以直接用因数个数计算得出。
去除重复答案(除了$n\times n$之外都计算了两次),可知$ans=\frac{d(n^2)+1}{2}$。
容斥原理与最小公倍数
首先给出最常用的两个函数。
int gcd(int x, int y){
return x%y==0 ? y:gcd(y, x%y);
}
int lcm(int x, int y){
return x*y/gcd(x, y);
}
n个集合的容斥原理
\[|A\cup B|=|A|+|B|-|A\cap B|\] \[|A\cup B\cup C| = |A| + |B| + |C|-|A\cap B|-|A\cap C|-|B\cap C| + |A\cap B\cap C|\] \[|A_1\cup A_2 \cup A_3 \cup ...A_{n-1} \cup A_n|\\=\sum\limits_i |A_i| - \sum\limits_{i<j}|A_i\cap A_j|+\sum\limits_{i<j<k}(A_i \cap A_j \cap A_k)-\sum\limits_{i<j<k<l}(A_i \cap A_j \cap A_k \cap A_l) ...\]也就是说,$n$元的容斥原理,是$O(2^n)$的。
习题
题面
三角形的 $2$ 条边上分别有 $m$ 和 $n$ 个点(不包括三角形的顶点),这些点分别同这两条边相对的顶点有连线,这样组成了一个复杂的图形,问这个图形中包含了多少个不同的三角形。由于数量很大,输出结果 $mod\ 1000000007$。
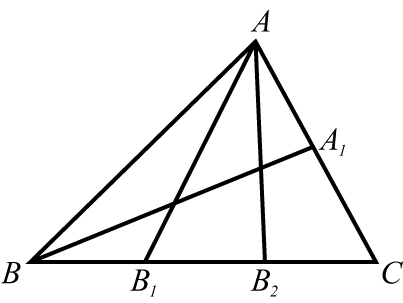
题解
若$AC$上有$m$个点,$BC$上有$n$个点。
考虑以$A$为顶点的三角形个数:$(m+1)\times C_{n+2}^2=(m+1)(n+2)(n+1)/2$
考虑以$B$为顶点的三角形个数:$(n+1)\times C_{m+2}^2=(n+1)(m+2)(m+1)/2$
再减去以$AB$为边的三角形个数:$(m+1)(n+1)$个即可。
取模与循环
\[(a*b)\mod p = [(a\mod p)*(b\mod p)] \mod p\]这种“分配律”对加法、减法、乘法成立,对除法不成立。
习题
题面
给出一个整数$N$,输出$N^N$的末位数字。
题解
直接模拟连乘对于$10^9$的数据范围会$TLE$。
考虑这件事:当一个$0-9$的数连乘自己时,末位数字必然出现循环。这可以理解为抽屉原理。
| 0-9的数 | 幂 mod 10 |
|---|---|
| 0 | [0] |
| 1 | [1] |
| 2 | [2,4,8,6] |
| 3 | [3,9,7,1] |
| 4 | [4,6] |
| 5 | [5] |
| 6 | [6] |
| 7 | [7,9,3,1] |
| 8 | [8,4,2,6] |
| 9 | [9,1] |
而且容易看出循环长度的最小公倍数是$4$。所以这题打表可做,复杂度$O(1)$。
#include `<iostream>`
using namespace std;
int a[10][4] = {{0,0,0,0},{1,1,1,1},{6,2,4,8},{1,3,9,7},{6,4,6,4},{5,5,5,5},{6,6,6,6},{1,7,9,3},{6,8,4,2},{1,9,1,9}};
// a[x][y]表示x(0<=x<=9)的(y+1)(0<=y<=3)次幂的末位
// y = n % 4 (前 n / 4 次幂是循环)
int main(){
int n;
cin >> n;
cout << a[n%10][n%4];
return 0;
}杨辉三角
| n/m | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 1 | ||||
| 1 | 1 | 1 | |||
| 2 | 1 | 2 | 1 | ||
| 3 | 1 | 3 | 3 | 1 | |
| 4 | 1 | 4 | 6 | 4 | 1 |
由上表可知,杨辉三角的第$n$行第$m$列对应着$C_n^m$。
所以容易推出$C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$。
杨辉三角还对应着二项式展开的系数:
\[(x+y)^n=\sum\limits_{i=0}^n C_n^ix^iy^{n-i}\]应用
从$(1,1)$走到$(m,n)$(只能向右或向上)的方案数为$C_{m+n-2}^{m-1}$。
康托展开(拓展)
康托展开是一个全排列到一个自然数的双射, 计算当前排列在所有由小到大全排列中的字典序。
\[X=a_n(n-1)!+a_{n-1}(n-2)!+...a_10!\]$a_i$表示原数的第 $i$ 位在当前未出现的元素中排在第几。
逆运算也成立,见下题。
习题(ProjectEuler 24)
#include <iostream>
#include <set>
using namespace std;
int fac[11];
set <int> nums;
set <int> ::iterator it;
void nclear(){
nums.clear();
for(int i=0;i<=9;i++){
nums.insert(i);
}
}//重置set
int main(){
int t, n, r;
fac[0]=fac[1]=1;
for(int i=2;i<10;i++){
fac[i] = i * fac[i-1];
}//预处理阶乘
cin >> t;
for(int i=1;i<=t;i++){
nclear();
cin >> n;
n--;
for(int i=9;i>0;i--){
r = n % fac[i];// 余数是下一位的 被除数
n /= fac[i]; // n 此时表示比这一位小的数的个数
int cnt=0;
for(it=nums.begin();cnt!=n&&it!=nums.end();it++){
cnt++;
}// 找到 此时的第 n 个数的迭代器
cout << *it;
nums.erase(it);
n = r;
}
cout << *nums.begin();
cout << endl;
}
return 0;
}
- 上一篇 暑期笔记 | STL中的简单数据结构 (线性表等)
- 下一篇 暑期笔记 | 刷题题解
♥