OI Diary 02:加快进度——充实的初升高暑假的开始
复盘
总结一下近期自己的时间轴:
2022.5.31 福州三中自招面试
2022.6.1-2022.6.24 中考复习 & 重学高中数学必修一
2022.6.25-2022.6.29 福建中考 & 学校毕业典礼
2022.6.30 福州三中自招预录取
2022.7.1-2022.7.5 经历手术 & 住院康复
2022.7.5-2022.7.8 在家开始重拾OI & 预习高中数理化
直到今天(2022.7.8),C++入门内容告一段落,接下来的就是一些基础算法。从课本来看,包括数据排序,递推算法,递归算法,回溯算法,广搜,深搜。
前两天在看C++入门内容的时候,为了赶进度,3h的录播课我一天能看3个……但是今天打开基础算法部分的第一课,我就意识到,似乎学习到这里就要开始动脑子了,而且时常要插上数位板用笔好好分析。
而且今天的课涉及到了排列组合,这对于学过奥数的小学生或许是小事,但是对经历了格式化中考的洗礼的初三毕业生来说还是有点强人所难了……所以我去看了两节讲排列组合的 高中数学网课 才活了过来TT
C++入门内容的刷题感觉刷的不够,但是为了赶进度就只能先这样了。下面总结一些做到的经典题吧。
归纳
高精度加法
实现高精度加法,输入输出等价于A+B Problem。
基本思路:
- 使用字符串来储存数字,并将位数较小的数前面用前导 “0” 补全,实现对齐。
- 模拟竖式加法的过程,即写下该位+进位。具体实现来看,就是在储存答案的字符串前推入
cnt%10,其中cnt是加法计数器。再将cnt/=10,便可把进位留到加法计数器中。
参考代码:
string add(string a, string b){
// 将 a, b 调整成位数较大的在前面,并对齐 a, b
int len_a=a.length(),len_b=b.length();
if(len_a<len_b) swap(a,b);
int len = a.length();
for(int i=1;i<=abs(len_a-len_b);i++) b="0"+b;
//做加法运算
string ans;
int cnt=0;
for(int i=len-1;i>=0;i--){
cnt+=a[i]-'0'+b[i]-'0';
ans=char(cnt%10+'0')+ans;
cnt/=10;
}
if(cnt) ans="1"+ans;//最高位的进位
return ans;
}
10进制整数转n进制数
除n取余,逆序输出
例如,要做(100)<sub>10</sub>转化为(X)<sub>2</sub>,可以使用短除法。
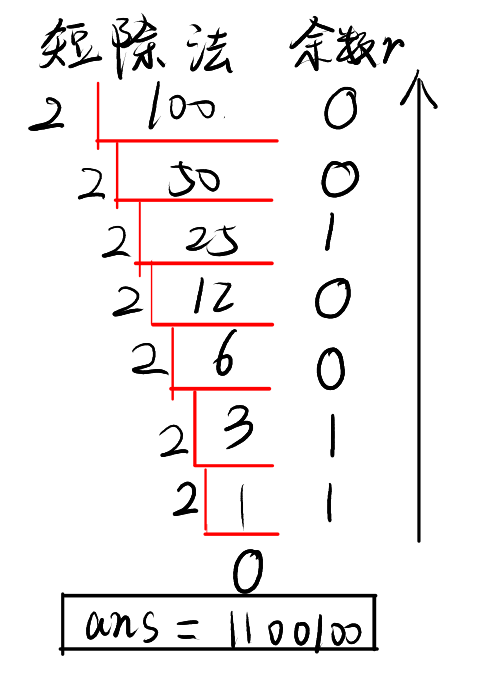
方法具有普适性,只要把除数替换成相应的进制数即可。
注意到,当余数大于等于10时,用字母代替,例如 10-A, 11-B, 12-C。这可以用 char x=num-10+'A' 实现。
输出m取n的所有排列和组合
初识深度优先搜索算法,很难写出具体要怎么理解。先放在这里,只能自己用心领会。
可以用树状图辅助理解。
int n,m,ans[101],vis[101];
//相当于A(n,m)
void put_a(int p){
if(p>n){
for(int i=1;i<=n;i++){
cout << ans[i] << " ";
}
cout << endl;
return;
}
for(int i=1;i<=m;i++){
if(vis[i]==0){
ans[p]=i;
vis[i]=1;
put_a(p+1);
vis[i]=0;
}
}
}
//相当于C(n,m)
void put_c(int p){
if(p>n){
for(int i=1;i<=n;i++){
cout << ans[i] << " ";
}
cout << endl;
return;
}
for(int i=ans[p-1]+1;i<=m;i++){
if(vis[i]==0){
ans[p]=i;
vis[i]=1;
put_c(p+1);
vis[i]=0;
}
}
}
♥