OI Diary 01:愚昧?大胆?追梦——初三从零开始学OI
复盘
无知者无畏?
是的,如题,我在一个微妙的时间点开始了我的OI之旅。这时距离我的中考,不到半年。
我有什么资本呢?没有。我的基本Code能力都不行,C++只会最基础最基础的语法,更别提数据结构和算法了。
我做好了失败并且浪费大量时间的心理准备,从寒假的第一天开始,上了5天的线下课(2022.1.22-1.56)。
在这期间,我得知了自己的期末考成绩,虽然看上去还可以(段4),但相比于连续三次的段1,我深知自己的状态正在下滑,尤其是语文已经掉到了惊人的段159,这让我越来越担心自己的一检乃至中考。这几次校考的难度都低得离谱,而一检——确是很难的。
直到现在,我仍然不确定自己能学到什么程度。在今天,我通过了最简单的第一期测试,希望这是一个好的开始。
我会在有必要的时候放弃继续NOIP(例如一检/二检掉到段60以外),同时,我会在BLOG上定期复盘近期的学习成果。
作为一个刚入门的真-蒟蒻,衷心祝各位大佬和自己2022 NOIP rp++!
归纳
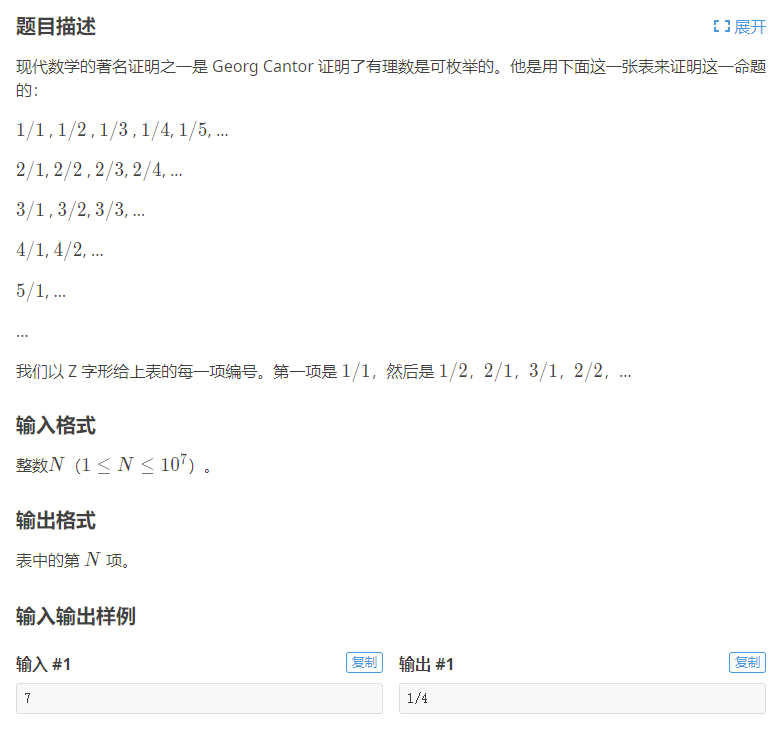
[NOIP1999 普及组] Cantor 表
基本思路:
模拟。首先理解Z字形编号的方法,将原表按照编号顺序转化为三角形表:
| k/p | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1/1 | |||
| 2 | 1/2 | 2/1 | ||
| 3 | 3/1 | 2/2 | 1/3 | |
| 4 | 1/4 | 2/3 | 3/2 | 4/1 |
观察到
-
三角形表的 第k行 正好有 k个数 。
-
对于任意 第k行 的 第p个数 ,都有它的 分子+分母=k+1。
-
如果 k为偶数 ,那么输出结果的分子就为 p ,分母为 k+1-p (k为奇数则分子分母颠倒)。
那么我们只需要知道第N个数在三角形表的第几行第几个即可,也就是要求出k和p。
(重点)可以考虑使用等差数列求和公式,符合条件的k值即为所求:
k*(k-1)/2 < N <= (1+k)*k/2
参考代码:
#include <cstdio>
using namespace std;
int main()
{
//定义变量+输入数据
int N,sum1,sum2,p,k=1;
scanf("%d",&N);
//判断 N 在第 k 行 第 p 个
while(!(sum1<N&&N<=sum2))
{
sum1 = k*(k-1)/2;
sum2 = (1+k)*k/2;
k++;
}
k--;
p = N-sum1;
//输出答案
printf("%d/%d\n",k%2==0?p:k+1-p,k%2==0?k+1-p:p);
return 0;
}
[知识点] 浮点数的处理
关于浮点数的运算,有两点需要知道:
- 如果我们需要比较两个浮点数的大小,使用
a>b?是不合适的,可能造成错误。要使用a-b>很小的数?(是否相等:abs(a-b)<很小的数?)。 - 有几个样例没过时,如果涉及浮点数运算,要考虑是否是浮点数精度造成的原因。
[知识点] 判断是否是质数时,只需要从2枚举到sqrt(x)
[算法] 辗转相除法(欧几里得算法)
计算最大公约数的方法。
定理:两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。
数学语言:gcd(a, b) = gcd(b, a mod b)
参考代码(递归):
int gcd(int a, int b)
{
return a%b==0 ? b : gcd(b, a%b);
}
END
- 上一篇 我使用了哪些数码产品?推荐&吐槽
- 下一篇 初中三年里,经历了两次网课?
♥